题目内容

20．已知一个几何体的三视图如图所示，则该几何体的表面积为（　　）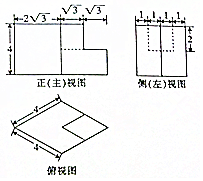
A．64+18$\sqrt{3}$B．64+16$\sqrt{3}$C．96D．92-2$\sqrt{3}$

分析 由已知中的三视图可得：该几何是一个以俯视图中大菱形为底面的四棱柱，切去一个以俯视图中小菱形为底面的四棱柱，得到的组合体，进而得到答案．

解答 解：由已知中的三视图可得：该几何是一个以俯视图中大菱形为底面的四棱柱，切去一个以俯视图中小菱形为底面的四棱柱，得到的组合体，
其表面积相当于大棱柱的表面积，
故S=2×$\frac{1}{2}$×4×4$\sqrt{3}$+4×4×4=64+16$\sqrt{3}$，
故选：B．

点评 本题考查的知识点是棱柱的体积和表面积，简单几何体的三视图，难度中档．

练习册系列答案
相关题目
10．已知$a={π^{\frac{1}{2}}}，b={log_π}\frac{1}{2}，c={log_{\frac{1}{π}}}\frac{1}{2}$，则（　　）
A．a＞b＞cB．a＞c＞bC．c＞b＞aD．c＞a＞b
11．等差数列{an}中，a1=13，a4=1，则公差d=-4．
8．（1）计算：8${\;}^{\frac{2}{3}}$+（$\frac{16}{81}$）${\;}^{-\frac{3}{4}}$-（$\sqrt{2}$-1）0；
（2）计算：9${\;}^{lo{g}_{9}2}$+$\frac{1}{3}$log68-2log${\;}_{{6}^{-1}}$$\sqrt{3}$．
15．已知函数f（x）=ax-lnx．
（1）过原点O作函数f（x）图象的切线，求切点的横坐标；
（2）对?x∈[1，+∞），不等式f（x）≥a（2x-x2）恒成立，求实数a的取值范围．
5．若函数f（x）=asinωx+bcosωx（0＜ω＜5，ab≠0）的图象的一条对称轴方程是$x=\frac{π}{4ω}$，函数f'（x）的图象的一个对称中心是$（{\frac{π}{8}，0}）$，则f（x）的最小正周期是（　　）
A．$\frac{π}{4}$B．$\frac{π}{2}$C．πD．2π
12．已知关于x的不等式$\frac{lo{g}_{a}x}{lnx}$-$\frac{4}{lnx}$＜lnx（a＞0且a≠1）对任意的x∈（1，100）恒成立，则实数a的取值范围为（0，1）∪（${e}^{\frac{1}{4}}$，+∞）．
9．如果过原点的直线l与圆x2+（y-4）2=4切于第二象限，那么直线l的方程是（　　）
A．$y=\sqrt{3}x$B．$y=-\sqrt{3}x$C．y=2xD．y=-2x
4．已知实数x，y满足5x2-y2-4xy=5，则2x2+y2的最小值是2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网