题目内容
2.下列函数中是奇函数,且最小正周期是π的函数是( )| A. | $y=cos({\frac{3π}{2}-2x})$ | B. | y=|cosx| | C. | $y=sin({\frac{π}{2}+2x})$ | D. | y=|sinx| |
分析 先判断函数的奇偶性,再求函数的周期,然后确定选项.
解答 解:对于A,y=cos($\frac{3π}{2}$-2x)=cos(π+$\frac{π}{2}$-2x)=-cos($\frac{π}{2}$-2x)=-sin2x,最小正周期为π,为奇函数,
对于B,y=|cosx|的最小正周期是π是偶函数,
对于C,y=sin($\frac{π}{2}$+2x)=cos2x的最小正周期是π是偶函数,
对于D,y=|sinx|的最小正周期是π是偶函数,
故选:A.
点评 本题考查三角函数的周期性及其求法,函数奇偶性的判断,考查计算能力,是基础题.

练习册系列答案
相关题目
10.已知$a={π^{\frac{1}{2}}},b={log_π}\frac{1}{2},c={log_{\frac{1}{π}}}\frac{1}{2}$,则( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | c>a>b |
17.已知函数f(x)是R上的偶函数,满足f(x)=-f(x+1),当x∈[2015,2016]时,f(x)=x-2017,则( )
| A. | $f(sin\frac{π}{3})>f(cos\frac{π}{3})$ | B. | f(sin2)>f(cos2) | C. | $f(sin\frac{π}{5})<f(cos\frac{π}{5})$ | D. | f(sin1)<f(cos1) |
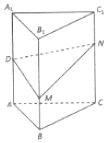 如图,正三棱柱ABC-A1B1C1的各棱长均相等,D为AA1的中点,M,N分别是线段BB1和线段CC1上的动点(含端点),且满足BM=C1N,当M,N运动时,下列结论中正确的序号为②③④.
如图,正三棱柱ABC-A1B1C1的各棱长均相等,D为AA1的中点,M,N分别是线段BB1和线段CC1上的动点(含端点),且满足BM=C1N,当M,N运动时,下列结论中正确的序号为②③④.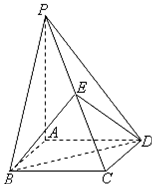 如图,四边形ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,E为PC中点.求证:平面BED⊥平面ABCD.
如图,四边形ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,E为PC中点.求证:平面BED⊥平面ABCD.