题目内容
 将数列{an}按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一个数a1,a2,a5,…构成公差为d的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为q的等比数列.若a1=1,a3=4,a5=3.
将数列{an}按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一个数a1,a2,a5,…构成公差为d的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为q的等比数列.若a1=1,a3=4,a5=3.(Ⅰ)求d,q的值;
(Ⅱ)求第n行各数的和T.
考点:数列的求和,归纳推理
专题:等差数列与等比数列
分析:(Ⅰ)依题意,可求得d=1,又a3=a2q=(a1+d)q,可求得q=2;
(Ⅱ)记第n行第1个数为A,易求A=n;据此数表的排列规律可知:每行的总个数构成一个以1为首项,2为公差的等差数列,而第n行共有(2n-1)个数,第n行各数为以n为首项,q=2为公比的等比数列,于是可求得第n行各数的和T.
(Ⅱ)记第n行第1个数为A,易求A=n;据此数表的排列规律可知:每行的总个数构成一个以1为首项,2为公差的等差数列,而第n行共有(2n-1)个数,第n行各数为以n为首项,q=2为公比的等比数列,于是可求得第n行各数的和T.
解答:
解:(Ⅰ)依题意得a5=a1+2d,∴3=1+2d,
所以d=1.…(2分)
又∵a3=a2q=(a1+d)q,q=2,
所以d,q的值分别为1,2.…(6分)
(Ⅱ)记第n行第1个数为A,
由(1)可知:A=a1+(n-1)d=n,…(7分)
又根据此数表的排列规律可知:每行的总个数构成一个以1为首项,2为公差的等差数列,
所以第n行共有(2n-1)个数,…(9分)
∴第n行各数为以n为首项,q=2为公比的等比数列,
因此其总数的和T=
=n•22n-1-n.…(12分)
所以d=1.…(2分)
又∵a3=a2q=(a1+d)q,q=2,
所以d,q的值分别为1,2.…(6分)
(Ⅱ)记第n行第1个数为A,
由(1)可知:A=a1+(n-1)d=n,…(7分)
又根据此数表的排列规律可知:每行的总个数构成一个以1为首项,2为公差的等差数列,
所以第n行共有(2n-1)个数,…(9分)
∴第n行各数为以n为首项,q=2为公比的等比数列,
因此其总数的和T=
| n(1-22n-1) |
| 1-2 |
点评:本题考查数列的求和,考查方程思想与运算推理能力,(Ⅱ)中判断出每行的总个数构成一个以1为首项,2为公差的等差数列是关键,突出考查归纳推理,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
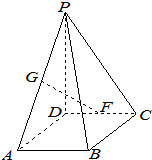 在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AB=1,BC=2,PD=
在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AB=1,BC=2,PD=