题目内容
2．变量x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ x-2y≤2\\ y≤0\end{array}\right.$，当目标函数z=2x-y取得最大值时，其最优解为（2，0）．分析 作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z的最优解．
解答 解：画出满足条件的平面区域，如图示：
，
由z=2x-y得：y=2x-z，
显然直线过A（2，0）时，z最大，
故答案为：（2，0）．
点评 本题主要考查线性规划的应用，利用图象平行求得目标函数的最大值和最小值，利用数形结合是解决线性规划问题中的基本方法．
练习册系列答案
53随堂测系列答案
相关题目
12．当x＞1时，关于函数f（x）=x+$\frac{1}{x-1}$，下列叙述正确的是（ ）
| A． | 函数f（x）有最小值2 | B． | 函数f（x）有最大值2 | C． | 函数f（x）有最小值3 | D． | 函数f（x）有最大值3 |
10．已知圆C：x2+y2-2x-1=0，直线l：3x-4y+12=0，圆C上任意一点P到直线l的距离小于2的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
7．在空间直角坐标系中，A（0，0，2），B（2，2，2），在平面xoy中找一点P，使得|PA|+|PB|最小，则点P的坐标为（ ）
| A． | （0，0，0） | B． | （2，2，0） | C． | （1，1，0） | D． | （0，1，0） |
14．已知复数z=$\frac{2}{1+i}$，则|z|等于（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | 2 $\sqrt{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
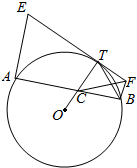已知AB是圆O的一条弦，过点A、B分别作AE⊥AB，BF⊥AB，交弧AB上任意一点T的切线于点E、F，OT交AB于点C，求证：