题目内容
4.已知函数f(x)=x2-3x-2lnx.(1)求函数f(x)的单调区间和极值;
(2)若函数g(x)=f(x)+alnx,求g(x)在区间[1,2]上的最大值.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)求出g(x)的导数,通过讨论a的范围,求出g(x)的单调性,从而求出其最大值即可.
解答 解:(1)f(x)的定义域是(0,+∞),
f′(x)=$\frac{(2x+1)(x-2)}{x}$,
令f′(x)>0,解得:x>2,令f′(x)<0,解得:0<x<2,
∴f(x)在(0,2)递减,在(2,+∞)递增;
(2)g(x)=f(x)+alnx=x2-3x+(a-2)lnx,
g′(x)=2x-3+$\frac{a-2}{x}$=$\frac{{2x}^{2}-3x+(a-2)}{x}$,
令h(x)=2x2-3x+(a-2),对称轴x=$\frac{3}{4}$,
h(x)在[1,2]递增,h(x)min=h(1)=a-3,h(x)max=h(2)=a,
①a≥3时,h(x)≥0,即g′(x)≥0,g(x)在[1,2]递增,
∴g(x)max=g(2)=(a-2)ln2-2,
②0<a<3时,?x0∈(1,2),
使得在[1,x0)h(x)<0,即g′(x)<0,g(x)递减,
在(x0,2],h(x)>0,即g′(x)>0,g(x)递增,
∴g(x)的最大值是g(1)或g(2),
③a≤0时,h(x)≤0,即g′(x)≤0,g(x)递减,
g(x)max=g(1)=(a-2)ln2-2,
综上,g(x)max=(a-2)ln2-2.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
12.设函数f(x)在R上存在导函数f′(x),对于任意的实数x,都有f(x)=4x2-f(-x),当x∈(-∞,0)时,f′(x)+$\frac{1}{2}$<4x,若f(m+1)≤f(-m)+4m+2,则实数m的取值范围是( )
| A. | [-$\frac{1}{2}$,+∞) | B. | [-$\frac{3}{2}$,+∞) | C. | [-1,+∞) | D. | [-2,+∞) |
19.等比数列-3,-6,…的第四项等于( )
| A. | -24 | B. | -9 | C. | -12 | D. | 24 |
9.某城市理论预测2007年到2011年人口总数与年份的关系如表所示
(1)请根据上表提供的数据,求最小二乘法求出Y关于x的线性回归方程;
(2)据此估计2016年该城市人口总数.
| 年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(2)据此估计2016年该城市人口总数.
7.若函数f(x)=$\frac{1}{3}$x3-(1+$\frac{b}{2}$)x2+2bx在区间[-3,1]上不是单调函数,则函数f(x)在R上的极小值为( )
| A. | 2b-$\frac{4}{3}$ | B. | $\frac{3}{2}$b-$\frac{2}{3}$ | C. | 0 | D. | b2-$\frac{1}{6}$b3 |
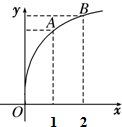 已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).
已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).