题目内容
2.若Cn3=Cn5,则n=8.分析 利用组合数的性质即可得出.
解答 解:∵Cn3=Cn5,
∴n=3+5=8.
故答案为:8.
点评 本题考查了组合数的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
13.把椭圆的普通方程9x2+4y2=36化为参数方程是( )
| A. | $\left\{\begin{array}{l}x=3cosθ\\ y=2sinθ\end{array}\right.(θ为参数)$ | B. | $\left\{\begin{array}{l}x=2cosθ\\ y=3sinθ\end{array}\right.(θ为参数)$ | ||
| C. | $\left\{\begin{array}{l}x=9cosθ\\ y=4sinθ\end{array}\right.(θ为参数)$ | D. | $\left\{\begin{array}{l}x=4cosθ\\ y=9sinθ\end{array}\right.(θ为参数)$ |
17.不等式$\frac{x-1}{{{x^2}-x-6}}$≥0的解集为( )
| A. | (-∞,-2)∪(3,+∞) | B. | (-∞,-2)∪[1,3) | C. | (-2,1]∪(3,+∞) | D. | (-2,1)∪[1,3) |
11.化简$\frac{cos(2π+α)tan(π+α)}{{cos(\frac{π}{2}-α)}}$的结果为 ( )
| A. | 1 | B. | -1 | C. | tanα | D. | -tanα |
12.设函数f(x)在R上存在导函数f′(x),对于任意的实数x,都有f(x)=4x2-f(-x),当x∈(-∞,0)时,f′(x)+$\frac{1}{2}$<4x,若f(m+1)≤f(-m)+4m+2,则实数m的取值范围是( )
| A. | [-$\frac{1}{2}$,+∞) | B. | [-$\frac{3}{2}$,+∞) | C. | [-1,+∞) | D. | [-2,+∞) |
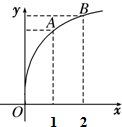 已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).
已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).