题目内容
9.函数y=sinx+$\sqrt{3}$cosx的最小值为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | -2 |
分析 利用两角和的正弦公式即可化为asinx+bcosx=$\sqrt{{a}^{2}+{b}^{2}}$sin(x+θ),进而利用正弦函数的单调性、最值即可得出.
解答 解:∵y=sinx+$\sqrt{3}$cosx=2($\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx)=2sin(x+$\frac{π}{3}$).
∵-1≤sin(x+$\frac{π}{3}$)≤1,
∴当sin(x+$\frac{π}{3}$)=-1时,函数y取得最小值-2.
故选:D.
点评 本题属于基础题,熟练掌握两角和的正弦公式化asinx+bcosx=$\sqrt{{a}^{2}+{b}^{2}}$sin(x+θ)、及正弦函数的单调性、最值是解题的关键.

练习册系列答案
相关题目
20.一元二次不等式-x2+4x+5<0的解集为( )
| A. | (-1,5) | B. | (-5,1) | C. | (-∞,-1)∪(5,+∞) | D. | (-∞,-5)∪(1,+∞) |
17.不等式$\frac{x-1}{{{x^2}-x-6}}$≥0的解集为( )
| A. | (-∞,-2)∪(3,+∞) | B. | (-∞,-2)∪[1,3) | C. | (-2,1]∪(3,+∞) | D. | (-2,1)∪[1,3) |
1.调查某桑场采桑员和辅助工关于桑毛虫皮炎发病情况结果如表:
(1)完成2×2列联表;
(2)利用2×2列联表的独立性检验估计,“患桑毛虫皮炎病与采桑”是否有关?
(参考公式:χ2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 采桑 | 不采桑 | 合计 | |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 |
(2)利用2×2列联表的独立性检验估计,“患桑毛虫皮炎病与采桑”是否有关?
| 参考数据 | 当χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当χ2>2.706时,有90%把握判定变量A,B有关联; | |
| 当χ2>3.841时,有95%把握判定变量A,B有关联; | |
| 当χ2>6.635时,有99%把握判定变量A,B有关联. |
19.等比数列-3,-6,…的第四项等于( )
| A. | -24 | B. | -9 | C. | -12 | D. | 24 |
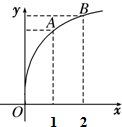 已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).
已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).