题目内容
6.下列函数中,最小正周期为$\frac{π}{2}$的是( )| A. | y=sinx | B. | y=cosx | C. | y=tan$\frac{x}{2}$ | D. | y=cos4x |
分析 找出C选项中的函数解析式中ω的值,代入周期公式T=$\frac{π}{|ω|}$,A,B,D三个选项解析式中ω的值,代入周期公式T=$\frac{2π}{|ω|}$,分别求出各项的最小正周期,即可作出判断.
解答 解:A、y=sinx,∵ω=1,∴T=$\frac{2π}{1}$=2π,本选项错误;
B、y=cosx,∵ω=1,∴T=$\frac{2π}{1}$=2π,本选项错误;
C、y=tan$\frac{x}{2}$,∵ω=$\frac{1}{2}$,∴T=$\frac{π}{\frac{1}{2}}$=2π,本选项错误;
D、y=cos4x,∵ω=4,∴T=$\frac{2π}{4}$=$\frac{π}{2}$,本选项正确.
综上知,D选项正确.
故选:D.
点评 此题考查了三角函数的周期性及其求法,涉及的知识有正切函数及正弦函数的周期性,熟练掌握周期公式是解本题的关键,属于基础题.

练习册系列答案
相关题目
17.不等式$\frac{x-1}{{{x^2}-x-6}}$≥0的解集为( )
| A. | (-∞,-2)∪(3,+∞) | B. | (-∞,-2)∪[1,3) | C. | (-2,1]∪(3,+∞) | D. | (-2,1)∪[1,3) |
1.调查某桑场采桑员和辅助工关于桑毛虫皮炎发病情况结果如表:
(1)完成2×2列联表;
(2)利用2×2列联表的独立性检验估计,“患桑毛虫皮炎病与采桑”是否有关?
(参考公式:χ2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 采桑 | 不采桑 | 合计 | |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 |
(2)利用2×2列联表的独立性检验估计,“患桑毛虫皮炎病与采桑”是否有关?
| 参考数据 | 当χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当χ2>2.706时,有90%把握判定变量A,B有关联; | |
| 当χ2>3.841时,有95%把握判定变量A,B有关联; | |
| 当χ2>6.635时,有99%把握判定变量A,B有关联. |
11.化简$\frac{cos(2π+α)tan(π+α)}{{cos(\frac{π}{2}-α)}}$的结果为 ( )
| A. | 1 | B. | -1 | C. | tanα | D. | -tanα |
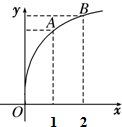 已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).
已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).