题目内容
19.某校教学大楼共有5层,每层均有2个楼梯,则由一楼至五楼的不同走法共有( )| A. | 24种 | B. | 52种 | C. | 10种 | D. | 7种 |
分析 通过层与层之间的走法,利用分步计数原理求解一层到五层的走法.
解答 解:共分4步:一层到二层 2种,二层到三层 2种,三层到四层 2种,四层到五层 2种,
一共24=16种.
故选A.
点评 本题主要考查分步计数原理的应用,理解好题意,从一层到五层共分四步.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
4.函数f(x)=2ax+1-3(a>0且a≠1)的图象经过的定点坐标是( )
| A. | (0,1) | B. | (-1,1) | C. | (-1,-1) | D. | (0,-3) |
11.化简$\frac{cos(2π+α)tan(π+α)}{{cos(\frac{π}{2}-α)}}$的结果为 ( )
| A. | 1 | B. | -1 | C. | tanα | D. | -tanα |
9.某城市理论预测2007年到2011年人口总数与年份的关系如表所示
(1)请根据上表提供的数据,求最小二乘法求出Y关于x的线性回归方程;
(2)据此估计2016年该城市人口总数.
| 年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(2)据此估计2016年该城市人口总数.
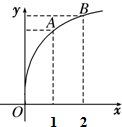 已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).
已知函数f(x)的图象如图所示,f'(x)是f(x)的导函数,将下列三个数值f(2)-f(1),f'(1),f'(2)由小到大排列顺序为f′(2)<f(2)-f(1)<f′(1).