题目内容
过双曲线
-x2=1的下焦点F作抛物线C：x2=2py（p＞0）的两条切线，切点分别为AB，若FA⊥FB，则抛物线的方程为（ ）
| y2 |
| 3 |
| A、x2=2y |
| B、x2=4y |
| C、x2=6y |
| D、x2=8y |
考点：双曲线的简单性质
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：求出双曲线的下焦点，由条件判断出切线方程为y=±x-2，代入抛物线方程，运用判别式为0，解方程即可得到抛物线方程．
解答：
解：双曲线
-x2=1的下焦点F（0，-2），
由FA⊥FB，
以及抛物线的对称性可得，
直线FA，FB的斜率为1和-1，
即有切线方程为y=±x-2，
代入抛物线方程x2=2py，可得，x2±2px+4p=0，
由判别式4p2-16p=0，
解得，p=4，
则有抛物线方程为x2=8y，
故选：D．
| y2 |
| 3 |
由FA⊥FB，
以及抛物线的对称性可得，
直线FA，FB的斜率为1和-1，
即有切线方程为y=±x-2，
代入抛物线方程x2=2py，可得，x2±2px+4p=0，
由判别式4p2-16p=0，
解得，p=4，
则有抛物线方程为x2=8y，
故选：D．
点评：本题考查双曲线的性质，考查抛物线的性质和方程，考查直线方程和抛物线方程联立，消去未知数，运用判别式为0，考查运算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
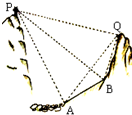如图，为了测量两座山峰上两点P、Q之间的距离，选择山坡上一段长度为300
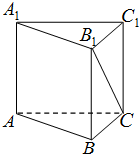如图，正三棱柱的底面边长为2，体积为
如图⊙O的直径为CA，OB⊥CA，M在OA上，连接BM交⊙O于N，以N为切点，作⊙O的切线交CA延长线于P．