题目内容
从1、2、3…n中任取三个不同的数,则取出的三个数可作为三角形三边边长的概率为 .(用n表示)
考点:古典概型及其概率计算公式
专题:计算题,概率与统计
分析:从1、2、3…n中任取三个不同的数,所有可能的组数为
=
;再以三边长中最长的边为标准分类,从而确定取出的三个数可作为三角形三边边长的组数,从而利用概率公式求概率.
| C | 3 n |
| n(n-1)(n-2) |
| 6 |
解答:
解:从1、2、3…n中任取三个不同的数,所有可能的组数为
=
;
不妨设所取的三个数为:c<b<a;
则由b+c>a知,
<b<a;
①当a为偶数,a≥4时,
+1≤b≤a-1;
又∵a-b<c<b;
∴a-b+1≤c≤b-1;
故c的可能取值个数为(b-1)-(a-b+1)+1=2b-a-1;
故b=a-1时,c的可能取值个数为a-3;
b=a-2时,c的可能取值个数为a-5;
…
b=
+1时,c的可能取值个数为1;
故1+3+5+…+(a-3)=(
)2;
②当a为奇数,a≥5时,
b=
+1.5时,c的可能取值个数为2;
b=
+2.5时,c的可能取值个数为4;
b=
+3.5时,c的可能取值个数为6;
…
b=a-1时,c的可能取值个数为a-3;
故2+4+6+…+a-3=(
)2+
;
故当n为偶数时,
取出的三个数可作为三角形三边边长的组数有
(12+22+…+(
)2)+(12+22+…+(
)2)+1+2+3+…+
=
;
故P=
×
=
,(n≥4);
故当n为奇数时,
取出的三个数可作为三角形三边边长的组数有
(12+22+…+(
)2)+(12+22+…+(
)2)+1+2+3+…+
=
;
故P=
×
=
,(n≥5).
故答案为:
,(n≥4,n为偶数),
,(n≥5,n为奇数).
| C | 3 n |
| n(n-1)(n-2) |
| 6 |
不妨设所取的三个数为:c<b<a;
则由b+c>a知,
| a |
| 2 |
①当a为偶数,a≥4时,
| a |
| 2 |
又∵a-b<c<b;
∴a-b+1≤c≤b-1;
故c的可能取值个数为(b-1)-(a-b+1)+1=2b-a-1;
故b=a-1时,c的可能取值个数为a-3;
b=a-2时,c的可能取值个数为a-5;
…
b=
| a |
| 2 |
故1+3+5+…+(a-3)=(
| a-2 |
| 2 |
②当a为奇数,a≥5时,
b=
| a |
| 2 |
b=
| a |
| 2 |
b=
| a |
| 2 |
…
b=a-1时,c的可能取值个数为a-3;
故2+4+6+…+a-3=(
| a-3 |
| 2 |
| a-3 |
| 2 |
故当n为偶数时,
取出的三个数可作为三角形三边边长的组数有
(12+22+…+(
| n-2 |
| 2 |
| n-4 |
| 2 |
| n-4 |
| 2 |
=
| n(n-2)(2n-5) |
| 24 |
故P=
| n(n-2)(2n-5) |
| 24 |
| 6 |
| n(n-1)(n-2) |
=
| 2n-5 |
| 4(n-1) |
故当n为奇数时,
取出的三个数可作为三角形三边边长的组数有
(12+22+…+(
| n-3 |
| 2 |
| n-3 |
| 2 |
| n-3 |
| 2 |
=
| (n-1)(n-3)(2n-1) |
| 24 |
故P=
| (n-1)(n-3)(2n-1) |
| 24 |
| 6 |
| n(n-1)(n-2) |
=
| (n-3)(2n-1) |
| 4n(n-2) |
故答案为:
| 2n-5 |
| 4(n-1) |
| (n-3)(2n-1) |
| 4n(n-2) |
点评:本题考查了排列组合的应用,同时考查了古典概型概率的求法,属于难题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设函数f(x)=
(a>0a≠1),其中[m]表示不超过m的最大整数,如[4.1]=4,则函数y=[f(x)-
]+[f(-x)-
]的值域是( )
| ax |
| 1+ax |
| 1 |
| 2 |
| 1 |
| 2 |
| A、{0,1} |
| B、{-1,1} |
| C、{-1,0} |
| D、{-1,0,1} |
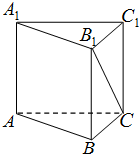 如图,正三棱柱的底面边长为2,体积为
如图,正三棱柱的底面边长为2,体积为 如图⊙O的直径为CA,OB⊥CA,M在OA上,连接BM交⊙O于N,以N为切点,作⊙O的切线交CA延长线于P.
如图⊙O的直径为CA,OB⊥CA,M在OA上,连接BM交⊙O于N,以N为切点,作⊙O的切线交CA延长线于P.