题目内容
椭圆
+
=1中,以点M(-1,2)为中点的弦所在的直线斜率为( )
| x2 |
| 16 |
| y2 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先设出弦的两端点的坐标,分别代入椭圆方程,两式相减后整理即可求得弦所在的直线的斜率.
解答:
解:设弦的两端点为A(x1,y1),B(x2,y2),
代入椭圆得
,
两式相减得
+
=0,
即
=-
,
即-
=
,
即-
=
,
即
=
,
∴弦所在的直线的斜率为
,
故选:B
代入椭圆得
|
两式相减得
| (x1-x2)(x1+x2) |
| 16 |
| (y1-y2)(y1+y2) |
| 9 |
即
| (x1-x2)(x1+x2) |
| 16 |
| (y1-y2)(y1+y2) |
| 9 |
即-
| 9(x1+x2) |
| 16(y1+y2) |
| y1-y2 |
| x1-x2 |
即-
| 9×(-2) |
| 16×4 |
| y1-y2 |
| x1-x2 |
即
| y1-y2 |
| x1-x2 |
| 9 |
| 32 |
∴弦所在的直线的斜率为
| 9 |
| 32 |
故选:B
点评:本题主要考查了椭圆的性质以及直线与椭圆的关系.在解决弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来,相互转化,达到解决问题的目的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
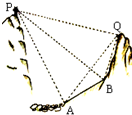 如图,为了测量两座山峰上两点P、Q之间的距离,选择山坡上一段长度为300
如图,为了测量两座山峰上两点P、Q之间的距离,选择山坡上一段长度为300 如图⊙O的直径为CA,OB⊥CA,M在OA上,连接BM交⊙O于N,以N为切点,作⊙O的切线交CA延长线于P.
如图⊙O的直径为CA,OB⊥CA,M在OA上,连接BM交⊙O于N,以N为切点,作⊙O的切线交CA延长线于P.