题目内容
已知函数y=（log2x）2-3•log2x2+3，x∈[1，2]的值域．
考点：对数的运算性质
专题：函数的性质及应用
分析：利用换元法将函数转化为一元二次函数即可得到结论．
解答：
解：y=（log2x）2-3•log2x2+3=（log2x）2-6•log2x+3，
设t=log2x，x∈[1，2]，
则0≤t≤1，
则函数等价为y=g（t）=t2-6•t+3=（t-3）2-6，在0≤t≤1上单调递减，
∴g（1）≤g（t）≤g（0），
即-2≤g（t）≤3，
∴函数的值域为[-2，3]．
设t=log2x，x∈[1，2]，
则0≤t≤1，
则函数等价为y=g（t）=t2-6•t+3=（t-3）2-6，在0≤t≤1上单调递减，
∴g（1）≤g（t）≤g（0），
即-2≤g（t）≤3，
∴函数的值域为[-2，3]．
点评：本题主要考查函数值域的计算，利用换元法转化为二次函数是解决本题的关键．
练习册系列答案
相关题目
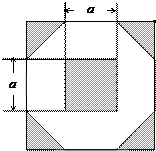为增加绿化面积，某小区将原来正方形地砖更换为如图所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为（ ）| A、2a2 |
| B、3a2 |
| C、4a2 |
| D、5a2 |
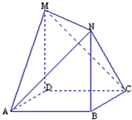四边形ABCD是边长为1的正方形，MD⊥平面ABCD，NB⊥平面ABCD，且MD=NB=1．