题目内容
设向量
=(a1,a2),
=(b1,b2),定义一种向量积
?
=(a1,a2)?(b1,b2)=(a1b1,a2b2).已知向量
=(2,
),
=(
,0),点P(x0,y0)为y=sinx的图象上的动点,点Q(x,y)为y=f(x)的图象上的动点,且满足
=
?
+
(其中O为坐标原点).
(Ⅰ)请用x0表示
?
;
(Ⅱ)求y=f(x)的表达式并求它的周期;
(Ⅲ)把函数y=f(x)图象上各点的横坐标缩小为原来的
倍(纵坐标不变),得到函数y=g(x)的图象.设函数h(x)=g(x)-t(t∈R),试讨论函数h(x)在区间[0,
]内的零点个数.
| a |
| b |
| a |
| b |
| m |
| 1 |
| 2 |
| n |
| π |
| 3 |
| OQ |
| m |
| OP |
| n |
(Ⅰ)请用x0表示
| m |
| OP |
(Ⅱ)求y=f(x)的表达式并求它的周期;
(Ⅲ)把函数y=f(x)图象上各点的横坐标缩小为原来的
| 1 |
| 4 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)直接根据所给新运算进行化简即可;
(Ⅱ)利用向量的相等,得到x0,y0与x,y之间的关系,然后建立关系式即可;
(Ⅲ)根据(Ⅱ),结合三角函数的图象与性质,分类讨论,确定零点的个数.
(Ⅱ)利用向量的相等,得到x0,y0与x,y之间的关系,然后建立关系式即可;
(Ⅲ)根据(Ⅱ),结合三角函数的图象与性质,分类讨论,确定零点的个数.
解答:
解:(Ⅰ)∵向量
=(2,
),
=(x0,y0),
∵点P(x0,y0)为y=sinx的图象上的动点,
∴y0=sinx0,
∴
?
=(2x0,
y0)=(2x0,
sinx0)
(Ⅱ)∵
=
?
+
所以(x , y)=(2x0 ,
sinx0)+(
,0)=(2x0+
,
sinx0),
因此
即
,
所以y=f(x)=
sin(
x-
),它的周期为4π.
(Ⅲ)g(x)=
sin(2x-
)在[0,
]上单调递增,在[
,
]上单调递减,
又g(0)=-
, g(
)=
, g(
)=
,
当t=
或-
≤t<
时,函数h(x)在区间[0,
]内只有一个零点;
当
≤t<
时,函数h(x)在区间[0,
]内有两个零点;
当t<-
或t>
时,函数h(x)在区间[0,
]内没有零点.
| m |
| 1 |
| 2 |
| OP |
∵点P(x0,y0)为y=sinx的图象上的动点,
∴y0=sinx0,
∴
| m |
| OP |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)∵
| OQ |
| m |
| OP |
| n |
所以(x , y)=(2x0 ,
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
因此
|
|
所以y=f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
(Ⅲ)g(x)=
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
又g(0)=-
| 1 |
| 4 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 4 |
当t=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| π |
| 2 |
当
| 1 |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
当t<-
| 1 |
| 4 |
| 1 |
| 4 |
| π |
| 2 |
点评:本题综合考查向量的基本运算,三角函数的图象与性质,函数的零点等知识,属于中档题.

练习册系列答案
相关题目
已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线x-y=0对称,则圆C2的方程为( )
| A、(x-1)2+(y+1)2=1 |
| B、(x-1)2+(y-1)2=1 |
| C、(x+1)2+(y+1)2=1 |
| D、(x+1)2+(y-1)2=1 |
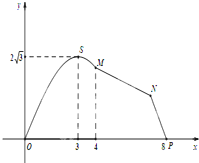 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asin(ωx)(A>0,ω>0),x∈[0,4]的图象,且图象的最高点为S(3,2
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asin(ωx)(A>0,ω>0),x∈[0,4]的图象,且图象的最高点为S(3,2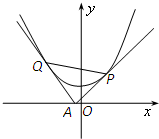 过x轴上动点A(a,0),引抛物线y=x2+1的两条切线AP、AQ.切线斜率分别为k1和k2,切点分别为P、Q.
过x轴上动点A(a,0),引抛物线y=x2+1的两条切线AP、AQ.切线斜率分别为k1和k2,切点分别为P、Q.