若两圆x2+y2=9与x2+y2-8x+6y-8a-25=0存在唯一公共点.求实数a的值．题目和参考答案——青夏教育精英家教网—

题目内容

若两圆x²+y²=9与x²+y²-8x+6y-8a-25=0存在唯一公共点，求实数a的值．

考点：圆与圆的位置关系及其判定

专题：直线与圆

分析：两个圆存在唯一公共点，利用两个圆的内切与外切，转化为圆心距等于半径和或差，求解即可．

解答： 解：∵x²+y²-8x+6y-8a-25=0的标准方程为：（x-4）²+（y+3）²=8a+50．圆的圆心坐标（4，-3），半径r=

50+8a

，（a＞-

）．
圆x²+y²=9的圆心（0，0），半径R=3，
圆x²+y²=9与x²+y²-8x+6y-8a-25=0存在唯一公共点，
∴

(4-0)2+(-3-0)2

=5=

50+8a

±3，
解得：a=-

或a=

．

点评：本题考查两个圆的位置关系的应用，圆心距与半径和与差的关系，基本知识的考查．

练习册系列答案

相关题目

，AB：AC=3：2，则sinB的值为（　　）

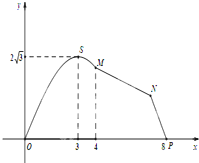如图，某市拟在长为8km的道路OP的一侧修建一条运动赛道，赛道的前一部分为曲线段OSM，该曲线段为函数y=Asin（ωx）（A＞0，ω＞0），x∈[0，4]的图象，且图象的最高点为S（3，2

），赛道的后一部分为折线段MNP，为保证参赛运动员的安全，限定∠MNP=120°．
（1）求A，ω的值和M，P两点间的距离；
（2）设∠PMN=θ，试用θ表示赛道MNP的长；
（3）当θ为何值时，折线段赛道MNP最长？

已知{a_n}是等差数列，若数列{b_n}满足b_n=a_2n-1+a_2n，证明：数列{b_n}为等差数列．

已知定点F（1，0），动点P（异于原点）在y轴上运动，连结PF，过点P作PM交x轴于点M，并延长MP与N，且

•

=0，|

|=|

|．
（1）求动点N的轨迹C的方程；
（2）若A（a，0），a∈R，求使|

|最小的点N的坐标．

已知函数y=（log₂^x）²-3•log₂^x²+3，x∈[1，2]的值域．

已知对于定义域为D的函数y=f（x），若同时满足下列条件：
①f（x）在D内单调递增或单调递减；
②存在区间[a，b]⊆D，使f（x）在[a，b]上的值域为[a，b]，
则把y=f（x）（x∈D）叫闭函数．
（1）求闭函数y=x²，x∈[0，+∞）符合条件②的区间[a，b]；
（2）是否存在函数f（x）=kx+b（k≠0）在R内为闭函数，且[1，2]为满足条件②的区间？若存在，求出f（x），若不存在，请说明理由．

已知奇函数f（x）是定义在[-1，1]上的增函数，且f（x-1）+f（1-3x）＞0，则x的取值范围是

．

试题分类