题目内容
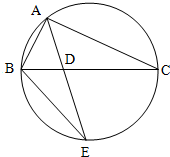如图所示，圆的两条弦AE，BC交于点D，且 |
| BE |
|
| CE |
（1）证明：AB•AC=AD•AE；
（2）若S△ABC=5，AD=2，AE=5，求∠BAC的大小．
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：（1）根据同弧、等弧所对的圆周角相等，可得∠BAE=∠CAE，∠C=∠E，从而△ABE∽△ADC，即可得出结论；（2）根据（1）的结论，再结合三角形面积公式S△ABC=
AB•ACsin∠BAC，不难得到∠BAC的大小．
| 1 |
| 2 |
解答：
（1）证明：∵
=
，
∴∠BAE=∠CAE，
∵∠C=∠E，
∴△ABE∽△ADC，
∴
=
，
∴AB•AC=AD•AE；
（2）解：∵AD=2，AE=5，
∴AB•AC=AD•AE=10．
∵S△ABC=
AB•ACsin∠BAC，S△ABC=5
∴sin∠BAC=1，
又∠BAC为三角形内角，
∴∠BAC=90°．
|
| BE |
|
| CE |
∴∠BAE=∠CAE，
∵∠C=∠E，
∴△ABE∽△ADC，
∴
| AB |
| AD |
| AE |
| AC |
∴AB•AC=AD•AE；
（2）解：∵AD=2，AE=5，
∴AB•AC=AD•AE=10．
∵S△ABC=
| 1 |
| 2 |
∴sin∠BAC=1，
又∠BAC为三角形内角，
∴∠BAC=90°．
点评：相似三角形有三个判定定理：判定定理1：两角对应相等的两个三角形相似； 判定定理2：三边对应成比例的两个三角形相似；判定定理3：两边对应成比例，并且夹角相等的两个三角形相似．在证明三角形相似时，要根据已知条件选择适当的定理．
练习册系列答案
相关题目