题目内容
设集合A={y|y=
，x≥0，且x≠1}，集合B={x|y=lg[x2-（2a+1）x+a2+a]，a∈R}．
（1）求集合A，B；
（2）若A∪B=R，求实数a的取值范围．
| 2x+1 |
| x-1 |
（1）求集合A，B；
（2）若A∪B=R，求实数a的取值范围．
考点：对数函数图象与性质的综合应用,并集及其运算
专题：函数的性质及应用,集合
分析：（1）根据不等式的解法，即可求出集合A，B．
（2）根据集合A∪B=R，建立不等式关系即可得到结论．
（2）根据集合A∪B=R，建立不等式关系即可得到结论．
解答：
解：（1）A={y|y=
，x≥0，且x≠1}=A={y|y=
=2+
，x≥0，且x≠1}={y|y≤-1或x＞2，
B={x|y=lg[x2-（2a+1）x+a2+a]，a∈R}={x|y=x2-（2a+1）x+a2+a＞0}={x|x＜a或x＞a+1}
（2）由A∪B=R得，a+1≤-1或a＞2，
即a≤-2或a＞2，
所以a∈（-∞，-2]∪（2，+∞）．
| 2x+1 |
| x-1 |
| 2(x-1)+3 |
| x-1 |
| 3 |
| x-1 |
B={x|y=lg[x2-（2a+1）x+a2+a]，a∈R}={x|y=x2-（2a+1）x+a2+a＞0}={x|x＜a或x＞a+1}
（2）由A∪B=R得，a+1≤-1或a＞2，
即a≤-2或a＞2，
所以a∈（-∞，-2]∪（2，+∞）．
点评：本题主要考查集合的基本运算，利用不等式的解法是解决本题的关键．
练习册系列答案
相关题目
如图，在四棱锥S-ABCD中，底面ABCD是矩形，AD=2AB，SA=SD，SA⊥AB，N是棱AD的中点．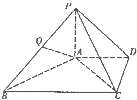
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，BC=2AD，PB⊥AC，Q是线段PB的中点．
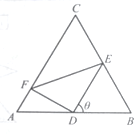如图，正三角形ABC的边长为2，D、E、F分别在三边AB，BC和CA上，且D为AB的中点，∠EDF=90°，∠BDE=θ（0°＜θ＜90°）．
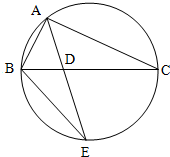如图所示，圆的两条弦AE，BC交于点D，且