题目内容

已知复数z1=a-2i，z2=b+i，
.
z1
是z1的共轭复数．若
.
z1
•z2=-4，则b=
 
．
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：把已知的复数代入
.
z1
•z2=-4，然后由复数代数形式的乘法运算化简后利用复数相等的条件列式求得b的值．
解答： 解：∵z1=a-2i，z2=b+i，
.
z1
是z1的共轭复数，
∴
.
z1
•z2=（a+2i）（b+i）=ab-2+（a+2b）i=-4．
∴
ab-2=-4
a+2b=0
，解得：b=±1．
故答案为：±1．
点评：本题考查了复数代数形式的乘法运算，考查了复数相等的条件，是基础题．
练习册系列答案
相关题目
已知f（x）=9x-2×3x+4，x∈[0，2]
（1）设t=3x，x∈[0，2]，求t的最大值与最小值；
（2）求f（x）的最大值与最小值．
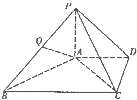如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，BC=2AD，PB⊥AC，Q是线段PB的中点．
（Ⅰ）求证：AB⊥平面PAC：
（Ⅱ）求证：AQ∥平面PC．
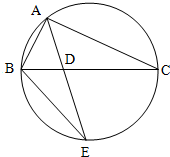如图所示，圆的两条弦AE，BC交于点D，且
BE
=
CE
．
（1）证明：AB•AC=AD•AE；
（2）若S△ABC=5，AD=2，AE=5，求∠BAC的大小．
已知实数x，y满足
x≤3
x+y-3≥0
x-y+1≥0
，则x2+y2的最小值是
 
．
已知函数f（x）=
x-k+2
x2+1
，若存在实数m∈[-1，1]，使得f（m）=1，则实数k的取值范围是
 
．
我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”，己知F1，F2是一对相关曲线的焦点，P是它们在第一象限的交点，当∠F1PF2=60°，则这 一对相关曲线中椭圆的离心率是
 
．
已知曲线C的极坐标方程为ρ=6sinθ，以极点为原点，极轴为x轴的非负半轴建立平面直角坐标系，直线l的参数方程为
x=
1
2
t
y=
3
2
t+1
（t为参数），求直线l被曲线C截得的线段长度
 
．
已知复数z=1-i（i为虚数单位），则复数z的模|z|=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网