题目内容
已知函数f(x)=x(
+
)
(1)判定并证明函数的奇偶性;
(2)试证明f(x)>0在定义域内恒成立;
(3)当x∈[1,3]时,2f(x)-(
)m•x<0恒成立,求m的取值范围.
| 1 |
| 2x-1 |
| 1 |
| 2 |
(1)判定并证明函数的奇偶性;
(2)试证明f(x)>0在定义域内恒成立;
(3)当x∈[1,3]时,2f(x)-(
| 1 |
| 2 |
考点:函数奇偶性的判断,函数恒成立问题
专题:综合题,函数的性质及应用
分析:(1)先求函数定义域,然后判断f(x)与f(-x)的关系,根据奇偶性的定义可作出判断;
(2)先利用指数函数的性质证明x>0时f(x)>0,然后利用偶函数的性质证明x<0时f(x)>0;
(3)2f(x)-(
)m•x<0对x∈[1,3]恒成立,分离参数后可得(
)m>2(
+
),令g(x)=2 (
+
),则问题化为g(x)max,利用基本函数的单调性可求得g(x)max;
(2)先利用指数函数的性质证明x>0时f(x)>0,然后利用偶函数的性质证明x<0时f(x)>0;
(3)2f(x)-(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2x-1 |
| 1 |
| 2 |
| 1 |
| 2x-1 |
| 1 |
| 2 |
解答:
解:(1)f(x)=x (
+
)为偶函数,证明如下:
f(x)=x (
+
)的定义域为:{x|x≠0}关于原点对称,
对于任意x∈{x|x≠0}有:f(-x)=-x (
+
)=x(
-
)=x(
-
)
=x (1+
-
)=x (
+
)=f(x)成立,
∴f(x)=x (
+
)为偶函数;
(2)∵f(x)=x (
+
)定义域为:{x|x≠0},
当x>0时,2x>20=1,∴2x-1>0,∴
+
>0,x>0,
∴f(x)=x(
+
)>0恒成立;
当x<0时,-x>0,由(1)可知:f(x)=f(-x)>0,
综上所述,f(x)>0在定义域内恒成立.
(3)2f(x)-(
)m•x<0对x∈[1,3]恒成立,
∴2x(
+
)-(
)m•x<0,∴(
)m>2(
+
),
令g(x)=2 (
+
),
当x∈[1,3]时,2x-1递增,
递减,
∴g(x)=2 (
+
)在[1,3]上为减函数,
∴g(x)=2 (
+
)≤g(1)=3对x∈[1,3]恒成立,
∴(
)m>3,解得m的取值范围是m<log
3.
| 1 |
| 2x-1 |
| 1 |
| 2 |
f(x)=x (
| 1 |
| 2x-1 |
| 1 |
| 2 |
对于任意x∈{x|x≠0}有:f(-x)=-x (
| 1 |
| 2-x-1 |
| 1 |
| 2 |
| 2x |
| 2x-1 |
| 1 |
| 2 |
| 2x-1+1 |
| 2x-1 |
| 1 |
| 2 |
=x (1+
| 1 |
| 2x-1 |
| 1 |
| 2 |
| 1 |
| 2x-1 |
| 1 |
| 2 |
∴f(x)=x (
| 1 |
| 2x-1 |
| 1 |
| 2 |
(2)∵f(x)=x (
| 1 |
| 2x-1 |
| 1 |
| 2 |
当x>0时,2x>20=1,∴2x-1>0,∴
| 1 |
| 2x-1 |
| 1 |
| 2 |
∴f(x)=x(
| 1 |
| 2x-1 |
| 1 |
| 2 |
当x<0时,-x>0,由(1)可知:f(x)=f(-x)>0,
综上所述,f(x)>0在定义域内恒成立.
(3)2f(x)-(
| 1 |
| 2 |
∴2x(
| 1 |
| 2x-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2x-1 |
| 1 |
| 2 |
令g(x)=2 (
| 1 |
| 2x-1 |
| 1 |
| 2 |
当x∈[1,3]时,2x-1递增,
| 1 |
| 2x-1 |
∴g(x)=2 (
| 1 |
| 2x-1 |
| 1 |
| 2 |
∴g(x)=2 (
| 1 |
| 2x-1 |
| 1 |
| 2 |
∴(
| 1 |
| 2 |
| 1 |
| 2 |
点评:该题考查函数的奇偶性、单调性的判断,考查恒成立问题的求解,考查转化思想,定义是研究函数基本性质的常用方法,要熟练掌握.

练习册系列答案
相关题目
已知向量
=(cosθ,sinθ),θ∈(
,π),
=(0,-1),则
与
的夹角等于( )
| a |
| π |
| 2 |
| b |
| a |
| b |
A、θ-
| ||
B、
| ||
C、
| ||
| D、θ |
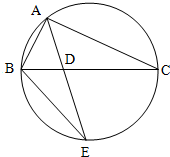 如图所示,圆的两条弦AE,BC交于点D,且
如图所示,圆的两条弦AE,BC交于点D,且