题目内容
若函数f(x)=
的定义域为(-∞,1],则实数a的值为 .
| 1+3x•a |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数f(x)的定义域,求出a的取值范围,再根据函数的解析式,求出a的取值范围,通过比较得出a的值来.
解答:
解:∵函数f(x)=
的定义域为(-∞,1],
∴1+3x•a≥0,
即3x•a≥-1,
∴a≥-1•(
)x;
又∵x≤1,
∴(
)x≥
,
∴-1×(
)x≤-
;
∴a的值为-
.
故答案为:-
.
| 1+3x•a |
∴1+3x•a≥0,
即3x•a≥-1,
∴a≥-1•(
| 1 |
| 3 |
又∵x≤1,
∴(
| 1 |
| 3 |
| 1 |
| 3 |
∴-1×(
| 1 |
| 3 |
| 1 |
| 3 |
∴a的值为-
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
点评:本题考查了函数的性质与应用的问题,解题时应根据函数的定义域以及函数的单调性进行解答,是基础题.

练习册系列答案
相关题目
甲、乙、丙、丁、戊和己6名学生进行劳动技术比赛,决出第一到第六名的名次.甲、乙两名参赛者去询问成绩,回答者对甲说“很遗憾,你和乙都没有得到冠军”,对乙说“你当然不会是最差的”.从上述回答分析,6人的名次排列可能有( )种不同情况.
| A、180 | B、288 |
| C、384 | D、480 |
一物体的运动方程为S=6t2+3t-2,则它在t=3时的瞬时速度为( )
| A、36 | B、39 | C、12 | D、33 |
已知函数f(x)=x2,则下列各式中正确的是( )
| A、f(-1)>f(2)>f(-3) |
| B、f(2)>f(-1)>f(-3) |
| C、f(-3)>f(2)>f(-1) |
| D、f(-3)>f(-1)>f(2) |
“m<
”是“方程x2+x+m=0有实数解”的( )
| 1 |
| 4 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
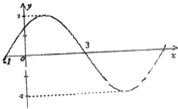 已知f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<
已知f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<