题目内容
3.已知变量x,y满足约束条件$\left\{\begin{array}{l}{2x-3y+6≥0}\\{2x-5y+10≤0}\\{x-6≤0}\end{array}\right.$则目标函数z=x+y的最大值为( )| A. | 12 | B. | $\frac{52}{5}$ | C. | $\frac{46}{5}$ | D. | 2 |
分析 画出约束条件表示的平面区域,根据图形找出最优解,求出目标函数的最大值.
解答 解:画出约束条件$\left\{\begin{array}{l}{2x-3y+6≥0}\\{2x-5y+10≤0}\\{x-6≤0}\end{array}\right.$表示的平面区域,如图所示;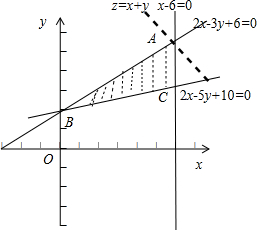
目标函数z=x+y化为y=-x+z,
由$\left\{\begin{array}{l}{x-6=0}\\{2x-3y+6=0}\end{array}\right.$,解得A(6,6);
所以目标函数z过点A时取得最大值,
为zmax=6+6=12.
故选:A.
点评 本题考查了简单的线性规划应用问题,是基础题.

练习册系列答案
相关题目
11.若“?x∈[1,2],使2x2-λx+1<0成立”是假命题,则实数λ的取值范围是( )
| A. | (-∞,2$\sqrt{2}$] | B. | [2$\sqrt{2}$,$\frac{9}{2}$] | C. | (-∞,3] | D. | [$\frac{9}{2}$,+∞) |
18.若角α的终边经过点(1,-5),则tanα等于( )
| A. | -5 | B. | 5 | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
8.关于函数$f(x)={log_{\frac{1}{2}}}|{\;x\;}|$,下列结论正确的是( )
| A. | 值域为(0,+∞) | B. | 图象关于x轴对称 | ||
| C. | 定义域为R | D. | 在区间(-∞,0)上单调递增 |