题目内容
已知P是双曲线
-
=1(a>0,b>0)右支上一点,F1,F2分别是双曲线的左、右焦点,I为△PF1F2的内心,若S△IPF1=S△IPF2+
S△IF1F2成立,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| A、4 | ||
B、
| ||
| C、2 | ||
D、2
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先根据题意作出示意图,如图所示,利用平面几何的知识利用三角形面积公式,代入已知式S△IPF1=S△IPF2+
S△IF1F2,化简可得|PF1|-|PF2|=
|F1F2|,再结合双曲线的定义与离心率的公式,可求出此双曲线的离心率.
| ||
| 2 |
| ||
| 2 |
解答:
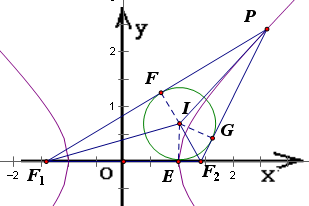 解:如图,设圆I与△PF1F2的三边F1F2、PF1、
解:如图,设圆I与△PF1F2的三边F1F2、PF1、
PF2分别相切于点E、F、G,连接IE、IF、IG,
则IE⊥F1F2,IF⊥PF1,IG⊥PF2,
它们分别是△IF1F2,△IPF1,△IPF2的高,
∴S△IPF1=
|PF1|•|IF|=
|PF1|,
S△IPF2=
|PF2|•|IG|=
|PF2|,
S△IF1F2=
|F1F2|•|IE|=
|F1F2|,
其中r是△PF1F2的内切圆的半径.
∵S△IPF2=S△IPF1-
S△IF1F2,
∴
|PF2|=
|PF1|-
|F1F2|,
两边约去
得:|PF2|=|PF1|-
|F1F2|,
∴|PF1|-|PF2|=
|F1F2|
根据双曲线定义,得|PF1|-|PF2|=2a,|F1F2|=2c,
∴2a=
c⇒离心率为e=
=
.
故选B.
 解:如图,设圆I与△PF1F2的三边F1F2、PF1、
解:如图,设圆I与△PF1F2的三边F1F2、PF1、PF2分别相切于点E、F、G,连接IE、IF、IG,
则IE⊥F1F2,IF⊥PF1,IG⊥PF2,
它们分别是△IF1F2,△IPF1,△IPF2的高,
∴S△IPF1=
| 1 |
| 2 |
| 1 |
| 2 |
S△IPF2=
| 1 |
| 2 |
| 1 |
| 2 |
S△IF1F2=
| 1 |
| 2 |
| 1 |
| 2 |
其中r是△PF1F2的内切圆的半径.
∵S△IPF2=S△IPF1-
| ||
| 2 |
∴
| r |
| 2 |
| r |
| 2 |
| ||
| 2 |
两边约去
| r |
| 2 |
| ||
| 2 |
∴|PF1|-|PF2|=
| ||
| 2 |
根据双曲线定义,得|PF1|-|PF2|=2a,|F1F2|=2c,
∴2a=
| 2 |
| c |
| a |
| 2 |
故选B.
点评:本题将三角形的内切圆放入到双曲线当中,用来求双曲线的离心率,着重考查了双曲线的基本性质、三角形内切圆的性质和面积计算公式等知识点,属于中档题.

练习册系列答案
相关题目
设集合S={x|x>2},T={x|-3≤x≤4},则S∩T=( )
| A、[4,+∞) |
| B、[3,+∞) |
| C、(2,4] |
| D、(2,3] |
已知函数f(x)=sin(2x-
)(x∈R),下面结论错误的是( )
| π |
| 3 |
| A、函数f(x)的最小正周期为π | ||
B、函数f(x)在区间[0,
| ||
| C、函数f(x)的图象关于直线x=0对称 | ||
D、函数f(x+
|
已知函数f(x)=sin(2ωx-
)(ω>0)的最小正周期为π,则函数f(x)的图象的一条对称轴方程是( )
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
某几何体的三视图如图所示,则t=x-y的取值范围是( )
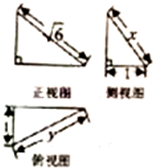

| A、[-4,4] | ||||
| B、(-1,1) | ||||
| C、[-1,1] | ||||
D、(1-
|
已知an=-2n2+9n+3,则数列{an}中的最大项为( )
| A、a1=10 |
| B、a2=13 |
| C、a3=12 |
| D、以上均不正确 |