题目内容
已知直线l的参数方程为
(t为参数).曲线C的极坐标方程为ρ=2
sin(θ+
).直线l与曲线C交于A,B两点,与y轴交于点P.
(1)求曲线C的直角坐标方程;
(2)求
+
的值.
|
| 2 |
| π |
| 4 |
(1)求曲线C的直角坐标方程;
(2)求
| 1 |
| |PA| |
| 1 |
| |PB| |
考点:直线的参数方程,参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(1)利用极坐标公式,把曲线C的极坐标方程ρ=2
sin(θ+
)化为ρ2=2ρsinθ+2ρcosθ,可得求曲线C的直角坐标方程;
(2)把直线的参数方程
(t为参数),代入曲线C的普通方程(x-1)2+(y-1)2=2中,得t2-t-1=0,利用参数的几何意义求
+
的值.
| 2 |
| π |
| 4 |
(2)把直线的参数方程
|
| 1 |
| |PA| |
| 1 |
| |PB| |
解答:
解:(1)利用极坐标公式,把曲线C的极坐标方程ρ=2
sin(θ+
)化为ρ2=2ρsinθ+2ρcosθ,…2分
∴直角坐标方程是x2+y2=2y+2x,…4分
即(x-1)2+(y-1)2=2…5分
(2)直线与曲线C交于A,B两点,与y轴交于点P,
把直线的参数方程
(t为参数),代入曲线C的普通方程(x-1)2+(y-1)2=2中,
得t2-t-1=0,…7分
∴
…8分
∴
+
=
+
=
=
=
…10分.
| 2 |
| π |
| 4 |
∴直角坐标方程是x2+y2=2y+2x,…4分
即(x-1)2+(y-1)2=2…5分
(2)直线与曲线C交于A,B两点,与y轴交于点P,
把直线的参数方程
|
得t2-t-1=0,…7分
∴
|
∴
| 1 |
| |PA| |
| 1 |
| |PB| |
| 1 |
| |t1| |
| 1 |
| |t2| |
| |t1-t2| |
| |t1•t2| |
| (t1+t2)2-4t1t2 |
| 5 |
点评:本题考查极坐标方程与直角坐标方程的互化,考查直线的参数方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
已知△ABC的顶点A(3,2),B(4,
),C(2,
),动点P(x,y)在△ABC的内部(包括边界),则
的取值是( )
| 3 |
| 3 |
| y |
| x-1 |
A、[
| ||||||
B、[1,
| ||||||
C、[
| ||||||
D、[
|
以下对正弦函数y=sinx的图象描述不正确的是( )
| A、在x∈[2kπ,2kπ+2π](k∈Z)上的图象形状相同,只是位置不同 |
| B、介于直线y=1与直线y=-1之间 |
| C、关于x轴对称 |
| D、与y轴仅有一个交点 |
设集合P={x|y=
+1},Q={y|y=x3},则P∩Q=( )
| x |
| A、∅ | B、[0,+∞) |
| C、(0,+∞) | D、[1,+∞) |
设变量x、y满足约束条件
,则z=2x-2y的最小值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知P是双曲线
-
=1(a>0,b>0)右支上一点,F1,F2分别是双曲线的左、右焦点,I为△PF1F2的内心,若S△IPF1=S△IPF2+
S△IF1F2成立,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| A、4 | ||
B、
| ||
| C、2 | ||
D、2
|
函数f(x)=2cos(x+
),x∈R的最小正周期为( )
| π |
| 6 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
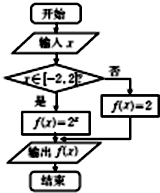 阅读如图所示的程序框图,如果输出的函数值在区间[
阅读如图所示的程序框图,如果输出的函数值在区间[| 1 |
| 4 |
| 1 |
| 2 |
| A、[-2,-1] |
| B、(-∞,-1] |
| C、[-1,2] |
| D、[2,+∞) |