题目内容
6.已知不等式x2+(6-a)x+9-3a>0,若该不等式对任意x∈[-2,0]恒成立,则a的取值范围是(-∞,1).分析 运用参数分离,结合x的范围,可得a<x+3,求出x+3的最小值,可得a的范围.
解答 解:不等式x2+(6-a)x+9-3a>0,
即为a(x+3)<x2+6x+9,
由x∈[-2,0],可得x+3∈[1,3],
即有a<x+3,
可得a<1.
故答案为:(-∞,1).
点评 本题考查不等式恒成立问题的解法,注意运用参数分离和函数的最值的求法,属于基础题.

练习册系列答案
相关题目
1.为了宣传2015年10月在贵阳举行的“世界众筹大会”,“世界众筹大会”筹委会举办了“大众创业、万众创新”知识有奖问答活动,随机对市民15~65岁的人群抽样n人,回答问题统计结果如图所示:
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖,各组抽取的人数分别是多少?
(3)请根据频率分布直方图,估计样本数据的众数和中位数.
| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | 频率分布直方图 |
| 第1组 | [15,25) | 5 | 0.5 | 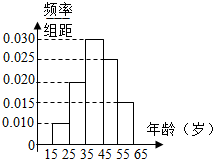 |
| 第2组 | [25,35) | a | 0.9 | |
| 第3组 | [35,45) | 27 | x | |
| 第4组 | [45,55) | 9 | 0.36 | |
| 第5组 | [55,65] | 3 | 0.2 |
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖,各组抽取的人数分别是多少?
(3)请根据频率分布直方图,估计样本数据的众数和中位数.
15.已知i是虚数单位,集合A={z|z=in,n∈N*},则A的子集个数有( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
18.为得到函数$y=2sin(2x+\frac{π}{4})$的图象,只需将函数y=2sin2x的图象( )
| A. | 向左平移$\frac{π}{4}$单位 | B. | 向右平移$\frac{π}{4}$单位 | C. | 向左平移$\frac{π}{8}$单位 | D. | 向右平移$\frac{π}{8}$单位 |