题目内容
17．已知成等比数列的三个数的积为27，和为13，求这三个数．分析 由题意可设这三个数为：$\frac{3}{q}$，3，3q，由和为13可得q的方程，解方程代入可得．
解答 解：∵成等比数列的三个数的积为27，
∴可设这三个数为：$\frac{3}{q}$，3，3q，
又∵这三个数的和为13，
∴$\frac{3}{q}$+3+3q=13，解得q=3或q=$\frac{1}{3}$，
分别代入计算可得这三个数为：1，3，9或9，3，1
点评 本题考查等差数列和等比数列的通项公式和性质，属基础题．
练习册系列答案
相关题目
8．
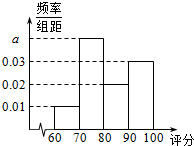某生产车间为了检测其加工的零件的质量，检验人员需抽取同批次的零件样本进行检测指标评分．若检测指标评分大于60分的零件为合格零件，指标评分不超过40分的零件将直接被淘汰，指标评分在（40，60]内的零件可能被修复也可能被淘汰．现质检员小张检测出200个合格零件，根据指标评分绘制的频率分布直方图如图所示，
（1）求出频率分布直方图中a的值；
（2）估计这200个零件指标评分的平均数和中位数；
（Ⅱ）根据已有的经验，可能被修复的零件个体被修复的概率如下表：
假设每个零件被修复与否相互独立．现有3个零件的检测指标评分（单位：分）为：38，45，52，
①求这3个零件中，至多有2个不被修复而淘汰的概率；
②记这3个零件被修复的个数为随机变量X，求X的分布列和数学期望．
某生产车间为了检测其加工的零件的质量，检验人员需抽取同批次的零件样本进行检测指标评分．若检测指标评分大于60分的零件为合格零件，指标评分不超过40分的零件将直接被淘汰，指标评分在（40，60]内的零件可能被修复也可能被淘汰．现质检员小张检测出200个合格零件，根据指标评分绘制的频率分布直方图如图所示，（1）求出频率分布直方图中a的值；
（2）估计这200个零件指标评分的平均数和中位数；
（Ⅱ）根据已有的经验，可能被修复的零件个体被修复的概率如下表：
| 零件检测指标评分所在区间 | （40，50] | （50，60] |
| 每个零件个体被修复的概率 | $\frac{1}{3}$ | $\frac{1}{2}$ |
①求这3个零件中，至多有2个不被修复而淘汰的概率；
②记这3个零件被修复的个数为随机变量X，求X的分布列和数学期望．
12．已知f（x）为奇函数，f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}（x+1），x∈[0，1）}\\{1-|x-3|，x∈[1，+∞）}\end{array}\right.$，方程f（x）=a（0＜a＜1）的所有实数根之和为（ ）
| A． | 1-2a | B． | 2a-1 | C． | （$\frac{1}{2}$）a-1 | D． | 1-（$\frac{1}{2}$）a |