题目内容
7. (Ⅰ)已知α角的终边经过点(t-2,t 2-1)且cosα≤0,sinα>0,求实数t的取值范围;
(Ⅰ)已知α角的终边经过点(t-2,t 2-1)且cosα≤0,sinα>0,求实数t的取值范围;(Ⅱ)试作出函数 $f(x)=\frac{sinx}{{|{sinx}|}}$在(-2π,2π)上的图象.
分析 (Ⅰ)直接根据α的终边在第二象限或y轴正向上,得到关于t的不等式组,解得即可,
(Ⅱ)先化为分段函数,再画图即可.
解答 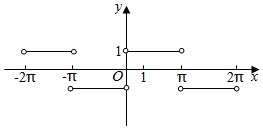 解:(Ⅰ)依题意,α的终边在第二象限或y轴正向上,∴$\left\{\begin{array}{l}t-2≤0\\{t^2}-1>0\end{array}\right.$$⇒\left\{\begin{array}{l}t≤2\\ t?-1或ora>1\end{array}\right.$,
解:(Ⅰ)依题意,α的终边在第二象限或y轴正向上,∴$\left\{\begin{array}{l}t-2≤0\\{t^2}-1>0\end{array}\right.$$⇒\left\{\begin{array}{l}t≤2\\ t?-1或ora>1\end{array}\right.$,
∴t<-1或1<t≤2.
(Ⅱ)$f(x)=\frac{sinx}{{|{sinx}|}}$=$\left\{\begin{array}{l}-1,x∈(-π,0)∪(π,2π)\\ 1,x∈(-2π,-π)∪(0,π)\end{array}\right.$
作出图象如图.
点评 本题考查了任意角的三角函数的定义以及函数图象的画法,属于基础题.

练习册系列答案
相关题目
16.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是两个互相垂直的单位向量,且$\overrightarrow{OA}$=$\frac{1}{4}$$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{OB}$=$\overrightarrow{{e}_{1}}$+$\frac{1}{2}$$\overrightarrow{{e}_{2}}$则$\overrightarrow{OA}$在$\overrightarrow{OB}$上的投影为( )
| A. | $\frac{{\sqrt{10}}}{4}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $\frac{{3\sqrt{5}}}{10}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
17.已知集合P={0,1},Q={0},则( )
| A. | Q=∅ | B. | P=Q | C. | P?Q | D. | P⊆Q |
 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.