题目内容
19.已知命题“p:?x∈[0,1],ex+a≥0”,命题“q:?x∈R,x2+x+a=0”,若命题“p∧q”为真命题,则实数a的取值范围为(-∞,-e].分析 命题“p:?x∈[0,1],ex+a≥0”,化为:a≤(-ex)min.命题“q:?x∈R,x2+x+a=0”,可得△≥0.利用命题“p∧q”为真命题,即可得出.
解答 解:命题“p:?x∈[0,1],ex+a≥0”,化为:a≤(-ex)min=-e.
命题“q:?x∈R,x2+x+a=0”,∴△=1-4a≥0,解得a≤$\frac{1}{4}$.
若命题“p∧q”为真命题,
则$\left\{\begin{array}{l}{a≤-e}\\{a≤\frac{1}{4}}\end{array}\right.$,解得a≤-e.
则实数a的取值范围为a≤-e.
故答案为:(-∞,-e].
点评 本题考查了一元二次方程的实数根与判别式的关系、函数的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
14.已知命题p:x2-4x+3<0与q:x2-6x+8<0;若“p且q”是不等式2x2-9x+a<0成立的充分条件,则实数a的取值范围是( )
| A. | (9,+∞) | B. | {0} | C. | (-∞,9] | D. | (0,9] |
11.某几何体的三视图如图所示,该几何体的体积是( )


| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 2 | D. | 4 |
8.一个空间几何体的三视图如图所示,则几何体的体积为( )


| A. | 2 | B. | $\frac{8}{3}$ | C. | 3 | D. | $\frac{10}{3}$ |
 (Ⅰ)已知α角的终边经过点(t-2,t 2-1)且cosα≤0,sinα>0,求实数t的取值范围;
(Ⅰ)已知α角的终边经过点(t-2,t 2-1)且cosα≤0,sinα>0,求实数t的取值范围;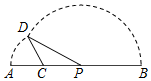 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为(2,4); f′(x)=0的解是3.
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为(2,4); f′(x)=0的解是3.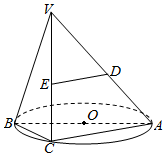 如图,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D、E分别是VA、VC的中点.
如图,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D、E分别是VA、VC的中点.