题目内容
12.若抛物线的焦点为$(0,-\frac{1}{2})$,则其标准方程为x2=-2y.分析 利用抛物线的性质求解.
解答 解:∵抛物线的焦点为$(0,-\frac{1}{2})$,
∴其标准方程为x2=-2y.
故答案为:x2=-2y.
点评 本题考查抛物线的标准方程的求法,是基础题,解题时要认真审题,注意抛物线性质的合理运用.

练习册系列答案
相关题目
17.曲线$f(x)=\frac{1}{3}{x^3}-2$在点$({1,-\frac{5}{3}})$处的斜率为( )
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | -1 | D. | 1 |
2.某几何体的三视图如图所示,则该几何体的表面积为( )
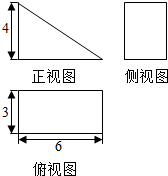

| A. | 36 | B. | $54+6\sqrt{13}$ | C. | $54+12\sqrt{5}$ | D. | $30+6\sqrt{73}$ |
 (Ⅰ)已知α角的终边经过点(t-2,t 2-1)且cosα≤0,sinα>0,求实数t的取值范围;
(Ⅰ)已知α角的终边经过点(t-2,t 2-1)且cosα≤0,sinα>0,求实数t的取值范围;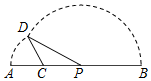 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为(2,4); f′(x)=0的解是3.
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为(2,4); f′(x)=0的解是3.