题目内容
2. 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.(1)求证:AC⊥平面PDB
(2)当PD=$\sqrt{2}$AB=2,设E为PB的中点,求AE与平面ABCD所成角.
分析 (1)根据题意证明AC⊥BD,PD⊥AC,可得AC⊥平面PDB;
(2)根据直线和平面所成角的定义找出直线和平面所成的角,即可得到结论.
解答 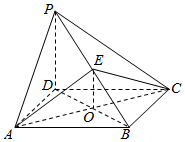 (1)证明:∵四边形ABCD是正方形,∴AC⊥BD,
(1)证明:∵四边形ABCD是正方形,∴AC⊥BD,
∵PD⊥底面ABCD,AC?底面ABCD,
∴PD⊥AC,
又BD∩PD=D,
∴AC⊥平面PDB,(3分)
(2)解:设AC∩BD=O,连接OE,由(1)知AC⊥平面PDB于O,
又O,E分别为DB、PB的中点,
∴OE∥PD,OE=$\frac{1}{2}$PD=$\frac{\sqrt{2}}{2}$,
∵PD⊥底面ABCD,
∴OE⊥底面ABCD,
则∴∠EAO为AE与平面ABCD所的角,
∵PD=$\sqrt{2}$AB=2,
∴PD=2,AB=$\sqrt{2}$,
在Rt△AOE中,OE=$\frac{\sqrt{2}}{2}$,
∵AB=$\sqrt{2}$,
∴A0=1,
∵AB=AO,
∴∠AEO=45°,(7分)
即AE与平面PDB所成的角的大小为45°.
点评 本题主要考查了直线与平面垂直的判定,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.已知$\overrightarrow{a}$=($\sqrt{3}$,-sinθ),$\overrightarrow{b}$=(-3,cosθ),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则角θ的值为( )
| A. | $\frac{π}{3}$+kπ(k∈Z) | B. | $\frac{π}{6}$+2kπ(k∈Z) | C. | $\frac{π}{3}$+2kπ(k∈Z) | D. | $\frac{π}{6}$+kπ(k∈Z) |
17.函数y=f(x)在(0,2)上是增函数,函数y=f(x+2)是偶函数,则下列结论正确的是( )
| A. | f(1)<f($\frac{5}{2}$)<f($\frac{7}{2}$) | B. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) | C. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) | D. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) |
14.已知命题p:x2-4x+3<0与q:x2-6x+8<0;若“p且q”是不等式2x2-9x+a<0成立的充分条件,则实数a的取值范围是( )
| A. | (9,+∞) | B. | {0} | C. | (-∞,9] | D. | (0,9] |
11.某几何体的三视图如图所示,该几何体的体积是( )


| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 2 | D. | 4 |
 (Ⅰ)已知α角的终边经过点(t-2,t 2-1)且cosα≤0,sinα>0,求实数t的取值范围;
(Ⅰ)已知α角的终边经过点(t-2,t 2-1)且cosα≤0,sinα>0,求实数t的取值范围;