题目内容
16.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是两个互相垂直的单位向量,且$\overrightarrow{OA}$=$\frac{1}{4}$$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{OB}$=$\overrightarrow{{e}_{1}}$+$\frac{1}{2}$$\overrightarrow{{e}_{2}}$则$\overrightarrow{OA}$在$\overrightarrow{OB}$上的投影为( )| A. | $\frac{{\sqrt{10}}}{4}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $\frac{{3\sqrt{5}}}{10}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
分析 把已知代入向量在向量方向上的投影公式,结合向量的数量积运算化简得答案.
解答 解:由题意知,$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}=0$,又$\overrightarrow{OA}$=$\frac{1}{4}$$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{OB}$=$\overrightarrow{{e}_{1}}$+$\frac{1}{2}$$\overrightarrow{{e}_{2}}$,
∴$\overrightarrow{OA}$在$\overrightarrow{OB}$上的投影为$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OB}|}=\frac{(\frac{1}{4}\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}})•(\overrightarrow{{e}_{1}}+\frac{1}{2}\overrightarrow{{e}_{2}})}{\sqrt{(\overrightarrow{{e}_{1}}+\frac{1}{2}\overrightarrow{{e}_{2}})^{2}}}$=$\frac{\frac{1}{4}+\frac{1}{2}}{\sqrt{1+\frac{1}{4}}}=\frac{3\sqrt{5}}{10}$.
故选:C.
点评 本题考查平面向量的数量积运算,考查了向量在向量方向上的投影的概念,是中档题.

练习册系列答案
相关题目
11.某几何体的三视图如图所示,该几何体的体积是( )


| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 2 | D. | 4 |
8.一个空间几何体的三视图如图所示,则几何体的体积为( )


| A. | 2 | B. | $\frac{8}{3}$ | C. | 3 | D. | $\frac{10}{3}$ |
6.在△ABC中,角A,B,C所对的边分别为a,b,c,且c=1,∠A=45°,S△ABC=2,则a=( )
| A. | 5 | B. | 25 | C. | $\sqrt{41}$ | D. | $5\sqrt{2}$ |
 (Ⅰ)已知α角的终边经过点(t-2,t 2-1)且cosα≤0,sinα>0,求实数t的取值范围;
(Ⅰ)已知α角的终边经过点(t-2,t 2-1)且cosα≤0,sinα>0,求实数t的取值范围;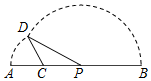 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为(2,4); f′(x)=0的解是3.
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为(2,4); f′(x)=0的解是3.