题目内容
已知
+
=1(a>b>0),M、N是椭圆的左、右顶点,P是椭圆上任意一点,且直线PM、PN的斜率分别为k1,k2(k1k2≠0),若|k1|+|k2|的最小值为1,且椭圆过点(
,
),则椭圆方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
A、
| ||
B、x2+
| ||
C、
| ||
D、
|
考点:椭圆的简单性质,椭圆的标准方程
专题:三角函数的求值,三角函数的图像与性质,圆锥曲线的定义、性质与方程
分析:首先把椭圆的方程转化为参数方程,进一步求出直线的斜率,利用最小值确定a和b的关系,最后求出椭圆的方程.
解答:
解:已知
+
=1(a>b>0),M、N是椭圆的左、右顶点,P是椭圆上任意一点,
设:P(acosα,bsinα),M(a,0),N(-a,0),
直线PM、PN的斜率分别为k1,k2(k1k2≠0),
则:|k1|+|k2|=
+
=
=
≥
,
|k1|+|k2|的最小值为1,
所以:
=1①
由于椭圆过点(
,
),
所以:
+
=1②
由①②得:椭圆的方程为:
+y2=1.
故选:C.
| x2 |
| a2 |
| y2 |
| b2 |
设:P(acosα,bsinα),M(a,0),N(-a,0),
直线PM、PN的斜率分别为k1,k2(k1k2≠0),
则:|k1|+|k2|=
| bsinα |
| a(1-cosα) |
| bsinα |
| a(1+cosα) |
| 2bsinα |
| asin2α |
| 2b |
| asinα |
| 2b |
| a |
|k1|+|k2|的最小值为1,
所以:
| 2b |
| a |
由于椭圆过点(
| 3 |
| 1 |
| 2 |
所以:
| 3 |
| a2 |
| ||
| b2 |
由①②得:椭圆的方程为:
| x2 |
| 4 |
故选:C.
点评:本题考查的知识要点:椭圆的参数式方程的应用,直线的斜率的应用,三角函数的变换,椭圆方程的确定.

练习册系列答案
相关题目
已知圆x2+y2=4与圆x2+y2-2y-6=0,则两圆的公共弦长为( )
A、
| ||
B、2
| ||
| C、2 | ||
| D、1 |
若命题“p∨q”与命题“¬p”都是真命题,则( )
| A、命p不一定是假命题 |
| B、命题q一定是真命题 |
| C、命题q不一定是真命题 |
| D、命题p与命题q同真同假 |
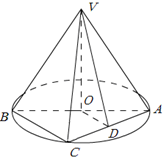 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.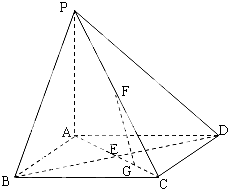 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为EC中点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为EC中点.