题目内容
10.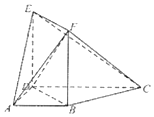 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD(1)求证:DF⊥CE
(2)若AC与BD相交于点O,那么在棱AE上是否存在点G,使得平面OBG∥平面EFC?并说明理由.
分析 (1)通过证明:DF⊥平面BCE,即可证明DF⊥CE
(2)棱AE上存在点G,$\frac{AG}{GE}$=$\frac{1}{2}$,使得平面OBG∥平面EFC,证明OB∥平面EFC,OG∥平面EFC,即可证明结论.
解答 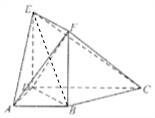 (1)证明:连接EB,
(1)证明:连接EB,
∵梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,
∴BD=$\sqrt{2}$,BC=$\sqrt{2}$,
∴BD2+BC2=CD2,
∴BC⊥BD,
∵平面BDEF丄平面ABCD,平面BDEF∩平面ABCD=BD,
∴BC⊥平面BDEF,
∴BC⊥DF,
∵DF⊥EB,EB∩BC=B,
∴DF⊥平面BCE,
∵CE?平面BCE,
∴DF⊥CE
(2)解:棱AE上存在点G,$\frac{AG}{GE}$=$\frac{1}{2}$,使得平面OBG∥平面EFC.
∵AB∥DC,AB=1,DC=2,
∴$\frac{AO}{OC}$=$\frac{1}{2}$,
∵$\frac{AG}{GE}$=$\frac{1}{2}$,
∴OG∥CE,
∵EF∥OB,
∴OB∥平面EFC,OG∥平面EFC,
∵OB∩OG=O,
∴平面OBG∥平面EFC.
点评 本题考查了线面平行,线面垂直的判断,考查面面平行的判定,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
20.已知函数f(x)=$\sqrt{3}$sin(ωx-$\frac{π}{6}$)-$\frac{1}{2}$(ω>0),函数图象的对称中心到对称轴的最小距离为$\frac{π}{4}$,将函数f(x)的图象向右平移$\frac{π}{12}$个单位长度得到函数g(x)的图象,若g(x)-3≤m≤g(x)+3在x∈[0,$\frac{π}{3}$]上恒成立,则实数m的取值范围是( )
| A. | [-2,1] | B. | [-5,1] | C. | [-2,4] | D. | [-5,4] |
1.已知等比数列{an}的前n项和Sn=$\frac{{4}^{n}-1}{3}$,则数列{$\sqrt{{a}_{n}}$}的前n项和Tn=( )
| A. | 2n-1 | B. | $\sqrt{\frac{{4}^{n}-1}{3}}$ | C. | $\frac{{2}^{n}-1}{3}$ | D. | $\frac{{2}^{n+1}-3}{3}$ |
18.已知平面α及直线a,b,则下列说法正确的是( )
| A. | 若直线a,b与平面α所成角都是30°,则这两条直线平行 | |
| B. | 若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直 | |
| C. | 若直线a,b平行,则这两条直线中至少有一条与平面α平行 | |
| D. | 若直线a,b垂直,则这两条直线与平面α不可能都垂直 |