题目内容
19.复数z=$\frac{a+i}{3+4i}$∈R,则实数a的值是$\frac{3}{4}$.分析 利用复数代数形式的乘除运算化简,再由虚部为0得答案.
解答 解:∵z=$\frac{a+i}{3+4i}$=$\frac{(a+i)(3-4i)}{(3+4i)(3-4i)}=\frac{(3a+4)+(3-4a)i}{25}$∈R,
∴3-4a=0,即a=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
9.某程序框图如图所示,若输出的p值为31,则判断框内应填入的不等式是( )
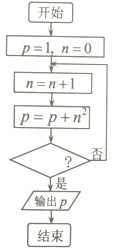

| A. | n>2 | B. | n>3 | C. | n>4 | D. | n>5 |
7.在△ABC中,∠ABC=120°,BA=2,BC=3,D,E是线段AC的三等分点,则$\overrightarrow{BD}$•$\overrightarrow{BE}$的值为( )
| A. | $\frac{65}{9}$ | B. | $\frac{11}{9}$ | C. | $\frac{41}{9}$ | D. | -$\frac{13}{9}$ |
4.设全集U=R,集合M={x|x2+x-2>0},$N=\left\{{x|{{(\frac{1}{2})}^{x-1}}≥2}\right\}$,则(∁UM)∩N=( )
| A. | [-2,0] | B. | [-2,1] | C. | [0,1] | D. | [0,2] |
11.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的两条渐进线与抛物线y2=4x的准线分别交于A,B两点,O为坐标原点,若${S_{△AOB}}=2\sqrt{3}$,则双曲线的离心率e=( )
| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | 2 | D. | $\sqrt{13}$ |
9.已知P1(2,-1),P2(0,5),点P在线段P1P2的延长线上,且|$\overrightarrow{{P}_{1}P}$|=2|$\overrightarrow{P{P}_{2}}$|,则点P的坐标( )
| A. | (4,-7) | B. | (-2,11) | C. | (4,-7)和(-2,11) | D. | (-2,11)和(1,2) |
10.等比数列{an}各项均为正数,且a5a6+a4a7=54,则log3a1+log3a2+…+log3a10=( )
| A. | 8 | B. | 10 | C. | 15 | D. | 20 |
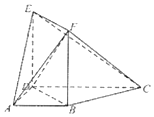 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD