题目内容
2.已知f(x)=x(2016+lnx),f′(x0)=2017,则x0等于1.分析 求函数的导数,利用方程关系进行求解即可.
解答 解:函数的导数f′(x)=2016+lnx+x•$\frac{1}{x}$=2017+lnx,
∵f′(x0)=2017,
∴f′(x0)=2017+lnx0=2017,则lnx0=0,
x0=1,
故答案为:1
点评 本题主要考查函数的导数的计算,根据条件求出函数的导数,解方程是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.在△ABC中,∠ABC=120°,BA=2,BC=3,D,E是线段AC的三等分点,则$\overrightarrow{BD}$•$\overrightarrow{BE}$的值为( )
| A. | $\frac{65}{9}$ | B. | $\frac{11}{9}$ | C. | $\frac{41}{9}$ | D. | -$\frac{13}{9}$ |
11.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的两条渐进线与抛物线y2=4x的准线分别交于A,B两点,O为坐标原点,若${S_{△AOB}}=2\sqrt{3}$,则双曲线的离心率e=( )
| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | 2 | D. | $\sqrt{13}$ |
13.函数y=x2cos x在x=1处的导数是( )
| A. | 0 | B. | 2cos1-sin 1 | C. | cos1-sin 1 | D. | 1 |
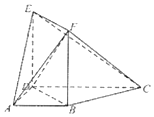 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD