题目内容
1.动直线l:y=kx-k+1(k∈R)经过的定点坐标为(1,1),若l和圆C:x2+y2=r2恒有公共点,则半径r的最小值是$\sqrt{2}$.分析 将直线化简成点斜式的形式得:y-1=k(x-1),可得直线的斜率为k且经过定点(1,1),利用定点在圆内,从而得到答案.
解答 解:将直线kx-y-k+1=0化简为点斜式,可得y-1=k(x-1),
∴直线经过定点(1,1),且斜率为k.
即直线kx-y-k+1=0(k∈R)恒过定点(1,1).
∵l和圆C:x2+y2=r2恒有公共点,
∴1+1≤r2,∴r≥$\sqrt{2}$,即半径r的最小值是$\sqrt{2}$
故答案为:(1,1),$\sqrt{2}$.
点评 本题给出含有参数k的直线方程,求直线经过的定点坐标.着重考查了直线的基本量与基本形式等知识,属于基础题.

练习册系列答案
相关题目
11.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的两条渐进线与抛物线y2=4x的准线分别交于A,B两点,O为坐标原点,若${S_{△AOB}}=2\sqrt{3}$,则双曲线的离心率e=( )
| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | 2 | D. | $\sqrt{13}$ |
9.已知P1(2,-1),P2(0,5),点P在线段P1P2的延长线上,且|$\overrightarrow{{P}_{1}P}$|=2|$\overrightarrow{P{P}_{2}}$|,则点P的坐标( )
| A. | (4,-7) | B. | (-2,11) | C. | (4,-7)和(-2,11) | D. | (-2,11)和(1,2) |
16.已知函数f(x)=-sin(x+$\frac{π}{2}$),(x∈R),下面结论错误的是( )
| A. | 函数f(x)的最小正周期为2π | B. | 函数f(x)在区间[0,$\frac{π}{2}$]上是增函数 | ||
| C. | 函数f(x)的图象关于直线x=0对称 | D. | 函数f(x)是奇函数 |
13.函数y=x2cos x在x=1处的导数是( )
| A. | 0 | B. | 2cos1-sin 1 | C. | cos1-sin 1 | D. | 1 |
10.等比数列{an}各项均为正数,且a5a6+a4a7=54,则log3a1+log3a2+…+log3a10=( )
| A. | 8 | B. | 10 | C. | 15 | D. | 20 |
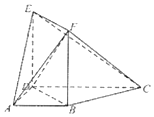 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD