题目内容
1.已知等比数列{an}的前n项和Sn=$\frac{{4}^{n}-1}{3}$,则数列{$\sqrt{{a}_{n}}$}的前n项和Tn=( )| A. | 2n-1 | B. | $\sqrt{\frac{{4}^{n}-1}{3}}$ | C. | $\frac{{2}^{n}-1}{3}$ | D. | $\frac{{2}^{n+1}-3}{3}$ |
分析 由等比数列{an}的前n项和求出首项和公比,进一步得到数列{$\sqrt{{a}_{n}}$}的首项和公比,再由等比数列的前n项和得答案.
解答 解:由Sn=$\frac{{4}^{n}-1}{3}$,得a1=S1=1;
当n≥2时,an=Sn-Sn-1=$\frac{{4}^{n}-1}{3}-\frac{{4}^{n-1}-1}{3}$=4n-1.
验证a1=1适合上式,
∴${a}_{n}={4}^{n-1}$,则等比数列{an}的公比q=$\frac{{a}_{n+1}}{{a}_{n}}=\frac{{4}^{n}}{{4}^{n-1}}=4$.
∴数列{$\sqrt{{a}_{n}}$}的首项为$\sqrt{{a}_{1}}=1$,公比为2.
∴数列{$\sqrt{{a}_{n}}$}的前n项和Tn=$\frac{1×(1-{2}^{n})}{1-2}={2}^{n}-1$.
故选:A.
点评 本题考查等比数列的前n项和,考查等比关系的确定,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.函数y=ex(2x-1)的大致图象是( )
| A. | 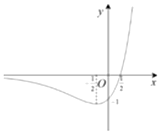 | B. | 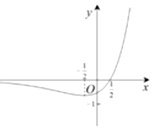 | ||
| C. | 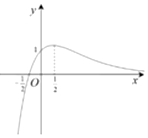 | D. | 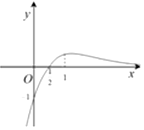 |
9.某程序框图如图所示,若输出的p值为31,则判断框内应填入的不等式是( )
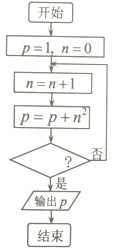

| A. | n>2 | B. | n>3 | C. | n>4 | D. | n>5 |
11.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的两条渐进线与抛物线y2=4x的准线分别交于A,B两点,O为坐标原点,若${S_{△AOB}}=2\sqrt{3}$,则双曲线的离心率e=( )
| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | 2 | D. | $\sqrt{13}$ |
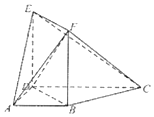 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD