题目内容
15.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|,0<x<2}\\{sin(\frac{π}{4}x),2≤x≤10}\end{array}\right.$,若存在实数x1,x2,x3,x4满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4,则$\frac{({x}_{3}-1)•({x}_{4}-1)}{{x}_{1}•{x}_{2}}$的取值范围是( )| A. | (9,21) | B. | (20,32) | C. | (8,24) | D. | (15,25) |
分析 画出函数f(x)的图象,确定x1x2=1,x3+x4=12,2<x3<x4<10,由此可得$\frac{({x}_{3}-1)•({x}_{4}-1)}{{x}_{1}•{x}_{2}}$的取值范围.
解答 解:函数的图象如图所示,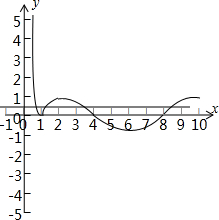
∵f(x1)=f(x2),
∴-log2x1=log2x2,
∴log2x1x2=0,
∴x1x2=1,
∵f(x3)=f(x4),
∴x3+x4=12,2<x3<x4<10
∴$\frac{({x}_{3}-1)•({x}_{4}-1)}{{x}_{1}•{x}_{2}}$=x3x4-(x3+x4)+1=x3x4-11,
∵2<x3<x4<10
∴$\frac{({x}_{3}-1)•({x}_{4}-1)}{{x}_{1}•{x}_{2}}$的取值范围是(9,21).
故选:A
点评 本小题主要考查分段函数的解析式求法及其图象的作法、函数的值域的应用、函数与方程的综合运用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于中档题.

练习册系列答案
相关题目
5.互联网背景下的“懒人经济”和“宅经济”渐成声势,推动了互联网餐饮行业的发展,而“80后”、“90后”逐渐成为餐饮消费主力,年轻人的餐饮习惯的改变,使省时、高效、正规的外送服务逐渐进入消费者的视野,美团外卖为了调查市场情况,对50人进行了问卷调查得到了如下的列联表,按照出生年龄,对喜欢外卖与否,采用分成抽样的方法抽取容量为10的样本,则抽到喜欢外卖的人数为6.
(Ⅰ)请将下面的列联表补充完整:
(Ⅱ)能否在犯错误的概率不超过0.005的前提下认为喜欢外卖与年龄有关?说明你的理由;
(Ⅲ)把“80后”中喜欢外卖的10个消费者从2到11进行编号,从中抽取一人,先后两次抛掷一枚骰子,出现的点数之和为被抽取的序号,试求抽到6号或10号的概率.
下面的临界值表供参考:
(参考公式:K2=$\frac{{n(ad-bc)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(Ⅰ)请将下面的列联表补充完整:
| 喜欢外卖 | 不喜欢外卖 | 合计 | |
| 90后 | 20 | 5 | 25 |
| 80后 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(Ⅲ)把“80后”中喜欢外卖的10个消费者从2到11进行编号,从中抽取一人,先后两次抛掷一枚骰子,出现的点数之和为被抽取的序号,试求抽到6号或10号的概率.
下面的临界值表供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
3.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点分別为A,B,点M,N是椭圆C上关于长轴对称的两点,若直线AM与BN相交于点P,则点P的轨迹方程是( )
| A. | x=±a(y≠0) | B. | y2=2b(|x|-a)(y≠0) | ||
| C. | x2+y2=a2+b2(y≠0) | D. | $\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(y≠0) |
20.执行如图所示的程序框图,则输出的S值是( )


| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -1 | D. | 4 |
7.在△ABC中,∠ABC=120°,BA=2,BC=3,D,E是线段AC的三等分点,则$\overrightarrow{BD}$•$\overrightarrow{BE}$的值为( )
| A. | $\frac{65}{9}$ | B. | $\frac{11}{9}$ | C. | $\frac{41}{9}$ | D. | -$\frac{13}{9}$ |
4.设全集U=R,集合M={x|x2+x-2>0},$N=\left\{{x|{{(\frac{1}{2})}^{x-1}}≥2}\right\}$,则(∁UM)∩N=( )
| A. | [-2,0] | B. | [-2,1] | C. | [0,1] | D. | [0,2] |
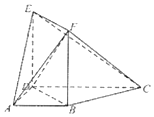 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD