题目内容
18.已知平面α及直线a,b,则下列说法正确的是( )| A. | 若直线a,b与平面α所成角都是30°,则这两条直线平行 | |
| B. | 若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直 | |
| C. | 若直线a,b平行,则这两条直线中至少有一条与平面α平行 | |
| D. | 若直线a,b垂直,则这两条直线与平面α不可能都垂直 |
分析 两条平行线可以和一个平面成相等的角;两条相交线可以和一个平面成相等的角;两条异面直线可以和一个平面成相等的角,可以判定A,B;
对C,显然错;
D,根据若两条直线与平面α都垂直,则线a,b平行,可以判断;
解答 解:对于A,若直线a,b与平面α所成角都是30°,则这两条直线平行、相交、异面,故错;
对于B,若直线a,b与平面α所成角都是30°,则这两条直线可能垂直,
如下图,直角三角形ACB的直角动点在平面α内,边AC、BC可以与平面都成300角,故错.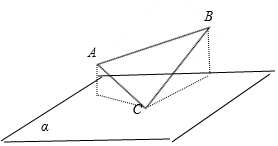
对于C,若直线a,b平行,则这两条直线中至少有一条与平面α平行,显然错;
对于D,若两条直线与平面α都垂直,则线a,b平行,故正确;
故选:D,
点评 本题考查两直线的位置关系的判断,直线与平面所成角位置关系的判断,是中档题,

练习册系列答案
相关题目
9.某程序框图如图所示,若输出的p值为31,则判断框内应填入的不等式是( )
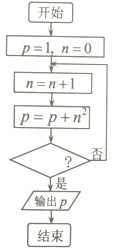

| A. | n>2 | B. | n>3 | C. | n>4 | D. | n>5 |
3.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点分別为A,B,点M,N是椭圆C上关于长轴对称的两点,若直线AM与BN相交于点P,则点P的轨迹方程是( )
| A. | x=±a(y≠0) | B. | y2=2b(|x|-a)(y≠0) | ||
| C. | x2+y2=a2+b2(y≠0) | D. | $\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(y≠0) |
7.在△ABC中,∠ABC=120°,BA=2,BC=3,D,E是线段AC的三等分点,则$\overrightarrow{BD}$•$\overrightarrow{BE}$的值为( )
| A. | $\frac{65}{9}$ | B. | $\frac{11}{9}$ | C. | $\frac{41}{9}$ | D. | -$\frac{13}{9}$ |
9.已知P1(2,-1),P2(0,5),点P在线段P1P2的延长线上,且|$\overrightarrow{{P}_{1}P}$|=2|$\overrightarrow{P{P}_{2}}$|,则点P的坐标( )
| A. | (4,-7) | B. | (-2,11) | C. | (4,-7)和(-2,11) | D. | (-2,11)和(1,2) |
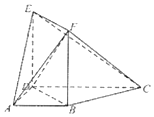 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD