题目内容
以下判断正确的是( )
| A、命题“负数的平方是正数”不是全称命题 |
| B、命题“?x∈N,x3>x2”的否定是“?x∈N,x3<x2” |
| C、“a=1”是函数f(x)=cos2ax-sin2ax的最小正周期为π的必要不充分条件 |
| D、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A,命题“负数的平方是正数”的含义为“任意一个负数的平方是正数”,是全称命题,可判断A;
B,写出命题“?x∈N,x3>x2”的否定,可判断B;
C,利用充分必要条件的概念,从充分性与必要性两个方面可判断C;
D,利用充分必要条件的概念与偶函数的定义可判断D.
B,写出命题“?x∈N,x3>x2”的否定,可判断B;
C,利用充分必要条件的概念,从充分性与必要性两个方面可判断C;
D,利用充分必要条件的概念与偶函数的定义可判断D.
解答:
解:对于A,命题“负数的平方是正数”是全称命题,故A错误;
对于B,命题“?x∈N,x3>x2”的否定是“?x∈N,x3≤x2”,故B错误;
对于C,a=1时,函数f(x)=cos2x-sin2x=cos2x的最小正周期为T=
=π,充分性成立;
反之,若函数f(x)=cos2ax-sin2ax=cos2ax的最小正周期T=
=π,则a=±1,必要性不成立;
所以“a=1”是函数f(x)=cos2ax-sin2ax的最小正周期为π的充分不必要条件,故C错误;
对于D,b=0时,函数f(-x)=ax2+bx+c=f(x),y=f(x)是偶函数,充分性成立;反之,若函数f(x)=ax2+bx+c是偶函数,f(-x)=f(x),解得a=0,即必要性成立;
所以“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件,故D正确.
故选:D.
对于B,命题“?x∈N,x3>x2”的否定是“?x∈N,x3≤x2”,故B错误;
对于C,a=1时,函数f(x)=cos2x-sin2x=cos2x的最小正周期为T=
| 2π |
| 2 |
反之,若函数f(x)=cos2ax-sin2ax=cos2ax的最小正周期T=
| 2π |
| 2|a| |
所以“a=1”是函数f(x)=cos2ax-sin2ax的最小正周期为π的充分不必要条件,故C错误;
对于D,b=0时,函数f(-x)=ax2+bx+c=f(x),y=f(x)是偶函数,充分性成立;反之,若函数f(x)=ax2+bx+c是偶函数,f(-x)=f(x),解得a=0,即必要性成立;
所以“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件,故D正确.
故选:D.
点评:本题考查命题的真假判断与应用,着重考查全称命题与特称命题之间的转化及充分必要条件的概念及应用,考查函数的周期性与奇偶性,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
已知函数f(x)=
是奇函数,则g(-4)的值等于( )
|
| A、-4 | B、-2 | C、2 | D、4 |
若某个几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线x2-
=1(b>0)的一条渐近线的方程为y=2x,则b的值等于( )
| y2 |
| b2 |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
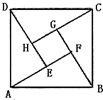 一次在北京召开的国际数学家大会,会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形,大正方形的面积是1,小正方形的面积是
一次在北京召开的国际数学家大会,会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形,大正方形的面积是1,小正方形的面积是