题目内容
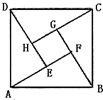一次在北京召开的国际数学家大会，会标如图所示，它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形，大正方形的面积是1，小正方形的面积是| 1 |
| 25 |
考点：几何概型
专题：概率与统计
分析：由已知大会会标由4个相同的直角三角形与中间的面积是 小正方形拼成的一个面积是1大正方形，我们可以设角形短直角边为x，然后根据余弦定理（在直角三角形中也可称为勾股定理），我们构造出关于x的方程，解方程求出三角形各边长，然后根据几何概型求概率．
解答：
解：设三角形较小直角边为x
∵S小正方形=
，
∴小正方形边长=
，
∴直角三角形另一条直角边为x+
，
∵S大正方形=1，
∴大正方形边长=1，
根据勾股定理，x2+（x+）2=12，
解得x=
，
所以AE=
+
=
，BF=
，
所以在线段AF与FB上任取一点P，则点P落在线段AF上的概率为
=
=
；
故答案为：
．
∵S小正方形=
| 1 |
| 25 |
∴小正方形边长=
| 1 |
| 5 |
∴直角三角形另一条直角边为x+
| 1 |
| 5 |
∵S大正方形=1，
∴大正方形边长=1，
根据勾股定理，x2+（x+）2=12，
解得x=
| 3 |
| 5 |
所以AE=
| 1 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
所以在线段AF与FB上任取一点P，则点P落在线段AF上的概率为
| BF |
| AF+BF |
| ||||
|
| 3 |
| 7 |
故答案为：
| 3 |
| 7 |
点评：本题考查的知识点是勾股定理几何概型、方程思想，根据已知，设出求知的边长，根据勾股定理构造出关于x的方程，是解答本题的关键．
练习册系列答案
相关题目
以下判断正确的是（ ）
| A、命题“负数的平方是正数”不是全称命题 |
| B、命题“?x∈N，x3＞x2”的否定是“?x∈N，x3＜x2” |
| C、“a=1”是函数f（x）=cos2ax-sin2ax的最小正周期为π的必要不充分条件 |
| D、“b=0”是“函数f（x）=ax2+bx+c是偶函数”的充要条件 |
已知f（x）为奇函数，g（x）为偶函数，且f（x）+g（x）=
，则f（3）=（ ）
| 1 |
| x-1 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
设点P在曲线y=ex上，点Q在曲线y=lnx上，则|PQ|的最小值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
对具有线性相关关系的变量x，y，测得一组数据如下表：
根据上表，利用最小二乘法得它们的回归直线方程为
=10.5x+a，则a的值等于（ ）
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
 |
| y |
| A、1 | B、1.5 | C、2 | D、2.5 |
如图所示，某程序图输出的果是（ ）
| A、17 | B、16 | C、15 | D、14 |