题目内容
求y=x-
的值域．
| x |
| 4 |
考点：函数的值域
专题：函数的性质及应用
分析：直接利用函数的定义域求函数的值域，利用函数的单调性求出结果．
解答：
解：已知y=x-
=
由于x∈R
且y=
在x∈R为单调递增函数．
所以y∈R
即函数的值域为：y∈R
| x |
| 4 |
| 3x |
| 4 |
由于x∈R
且y=
| 3x |
| 4 |
所以y∈R
即函数的值域为：y∈R
点评：本题考查的知识要点：函数的单调性的应用，属于基础题型．
练习册系列答案
相关题目
已知向量
=（2，3），
=（-2，x），若
在
方向上的投影等于-
，则实数x的值为（ ）
| a |
| b |
| a |
| b |
| ||
| 5 |
A、
| ||
| B、1 | ||
C、1或
| ||
| D、2 |
以下判断正确的是（ ）
| A、命题“负数的平方是正数”不是全称命题 |
| B、命题“?x∈N，x3＞x2”的否定是“?x∈N，x3＜x2” |
| C、“a=1”是函数f（x）=cos2ax-sin2ax的最小正周期为π的必要不充分条件 |
| D、“b=0”是“函数f（x）=ax2+bx+c是偶函数”的充要条件 |
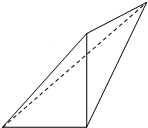一个四面体如图，若该四面体的正视图（主视图）、侧视图（左视图）和俯视图都是直角边长为1的等腰直角三角形，则它的体积V=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
若双曲线
-
=1（a＞0，b＞0）与直线y=
x无交点，则
的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| b |
| a |
A、（0，
| ||
B、（0，
| ||
C、（
| ||
D、[
|