题目内容
不等式2x2-9x+m≤0对x∈[2,3]总成立,求实数m的范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:构造函数f(x)=2x2-9x+m,利用二次函数的性质将不等式2x2-9x+m≤0对x∈[2,3]总成立转化为
,解不等式组即可得到实数m的范围.
|
解答:
解:令f(x)=2x2-9x+m,
则由二次函数性质知,
不等式2x2-9x+m≤0对x∈[2,3]总成立等价于
,
即
.
解得m≤9.
∴实数m的范围是(-∞,9].
则由二次函数性质知,
不等式2x2-9x+m≤0对x∈[2,3]总成立等价于
|
即
|
解得m≤9.
∴实数m的范围是(-∞,9].
点评:本题考查构造函数,利用函数的性质解决不等式恒成立问题的方法和技巧,属于中档题.

练习册系列答案
相关题目
在△ABC中,下列式子不正确的是( )
| A、a2=b2+c2-2bccosA | ||
| B、a:b:c=sinA:sinB:sinC | ||
C、S△ABC=
| ||
| D、b=2RsinB |
将下列各式按大小顺序排列,其中正确的是( )
A、cos0<cos
| ||
B、cos0<cos
| ||
C、cos0>cos
| ||
D、cos0>cos
|
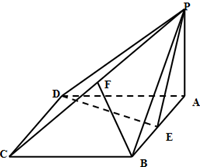 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.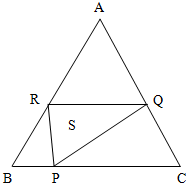 如图,在正△ABC的边BC、CA、AB上分别取点P、Q、R,使CQ=2BP,AR=3BP.已知正三角形的边长是11cm,BP=xcm,△PQR的面积为S
如图,在正△ABC的边BC、CA、AB上分别取点P、Q、R,使CQ=2BP,AR=3BP.已知正三角形的边长是11cm,BP=xcm,△PQR的面积为S