题目内容
定义某种运算?,a?b的运算原理如图所示,设f(x)=(0?x)x-(2?x).f(2)= .


考点:程序框图
专题:图表型
分析:通过程序框图判断出S=a?b的解析式,再求出f(x)的解析式,从而求出f(x)的解析式,最后令x=2即可.
解答:
解:∵由流程图可知,运算S=a?b中S的值等于分段函数
S=
的函数值,
∵f(x)=(0?x)x-(2?x),
∴f(2)=(0?2)×2-(2?2)=0×2-2=-2.
故答案为:-2.
S=
|
∵f(x)=(0?x)x-(2?x),
∴f(2)=(0?2)×2-(2?2)=0×2-2=-2.
故答案为:-2.
点评:本题考查选择结构,主要考查了判断程序框图的功能即判断出新运算法则,利用运算法则求值.解决新定义题关键是理解题中给的新定义.

练习册系列答案
相关题目
若ax2+4ax+3≥0恒成立,a的取值范围是( )
A、(0,
| ||
B、(0,
| ||
C、[0,
| ||
D、[0,
|
已知集合A={(x,y)||x|≤2,|y|≤2,x,y∈Z},集合B={(x,y)|(x-2)2+(y-2)2≤4,x,y∈Z},在集合A中任取一个元素p,则p∈B的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
集合A={x∈R|0<x≤2},B={x∈R|x2-x-2>0},则A∩(CRB)=( )
| A、(-1,2) |
| B、[-1,2] |
| C、(0,2) |
| D、(0,2] |
多项式1-a2-b2+2ab分解因式的结果是( )
| A、(1-a-b)(1+a+b) |
| B、(1+a-b)(1-a+b) |
| C、(a+b+1)(a-b-1) |
| D、-(a-b+1)(a+b-1) |
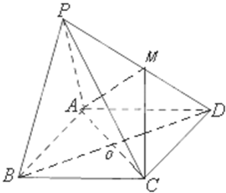 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知