题目内容
已知集合A={(x,y)||x|≤2,|y|≤2,x,y∈Z},集合B={(x,y)|(x-2)2+(y-2)2≤4,x,y∈Z},在集合A中任取一个元素p,则p∈B的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:因为x,y∈Z,且|x|≤2,|y|≤2,基本事件是有限的,所以为古典概型,这样求得总的基本事件的个数,再求得满足x,y∈Z,且(x-2)2+(y-2)2≤4的基本事件的个数,然后求比值即为所求的概率.
解答:
解:如图,点P所在的区域为正方形ABCD的内部(含边界)的整数点,共有5×5=25,
满足(x-2)2+(y-2)2≤4的点的区域为以(2,2)为圆心,2为半径的圆面(含边界)的整数点,有(0,2),(1,1),(1,2),(2,0),(2,1),(2,2),共6个.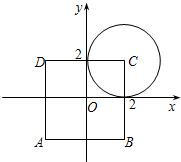
∴所求的概率为P=
故选C.
满足(x-2)2+(y-2)2≤4的点的区域为以(2,2)为圆心,2为半径的圆面(含边界)的整数点,有(0,2),(1,1),(1,2),(2,0),(2,1),(2,2),共6个.

∴所求的概率为P=
| 6 |
| 25 |
故选C.
点评:本题考查古典概型,考查等可能事件的概率,确定基本事件的个数是关键.

练习册系列答案
相关题目
已知集合M={0,2,4,6},集合Q={0,1,3,5},则M∪Q等于( )
| A、{0} |
| B、{0,1,2,3,4,5,6} |
| C、{1,2,3,4,5,6,} |
| D、{0,3,4,5,6} |
