题目内容
二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与点(0,-2),
(Ⅰ)求矩阵M;
(Ⅱ)设直线l在变换M作用下得到了直线m:x-2y=4,求直线l的方程.
(Ⅰ)求矩阵M;
(Ⅱ)设直线l在变换M作用下得到了直线m:x-2y=4,求直线l的方程.
考点:二阶矩阵
专题:矩阵和变换
分析:本题(Ⅰ)根据条件得到关于矩阵的方程,解方程组得到本题结论;(Ⅱ)利用矩阵变换得到变换前后的坐标关系,用代入法求出所得直线方程,得到本题结论.
解答:
解:(Ⅰ)设矩阵M=
,
则:
=
,
=
,
即
,
解得
∴M=
.
(Ⅱ)设(x,y)经M的变换作用后变为(x',y'),
则:
又∵x'-2y'=4,
∴(x+2y)-2(3x+4y)=4,
∴5x+6y+4=0.
即直线l的方程为:5x+6y+4=0.
|
则:
|
|
|
|
|
|
即
|
解得
|
∴M=
|
(Ⅱ)设(x,y)经M的变换作用后变为(x',y'),
则:
|
又∵x'-2y'=4,
∴(x+2y)-2(3x+4y)=4,
∴5x+6y+4=0.
即直线l的方程为:5x+6y+4=0.
点评:本题考查了矩阵变换与直线方程,本题难度不大,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
数列{an}的通项公式为an=ncos
,其前n项和为Sn,则S2015等于( )
| nπ |
| 2 |
| A、1002 | B、1004 |
| C、1006 | D、-1008 |
一个盛满水的三棱锥容器S-ABC中,不久发现三条侧棱上各有一个小洞D,E,F,且知SD:DA=SE:EB=CF:FS=2:1,若仍用这个容器盛水,则最多可盛原来水的( )
A、
| ||
B、
| ||
C、
| ||
D、
|
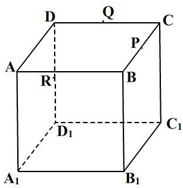 如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题: