题目内容
若方程x2+y2-6x+2y+F=0是圆的方程，则F的取值范围为 ．
考点：二元二次方程表示圆的条件
专题：圆锥曲线的定义、性质与方程
分析：由二元二次方程表示圆的条件得到F的不等式，解不等式即可得到结果．
解答：
解：方程x2+y2-6x+2y+F=0表示一个圆，
则36+4-4F＞0，
∴F＜10
故答案为：（-∞，10）．
则36+4-4F＞0，
∴F＜10
故答案为：（-∞，10）．
点评：本题考查二元二次方程表示圆的条件，属基础知识的考查，本题解题的关键是看清楚所表示的二元二次方程的各个系数之间的关系．
练习册系列答案
相关题目
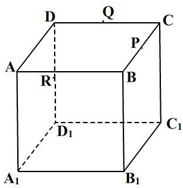如图，正方体ABCD-A1B1C1D1的棱长为2，P，Q，R分别是棱BC，CD，DD1的中点．下列命题：已知正六棱柱的高为6，底面边长为3，则它的体积为（ ）
| A、48 | ||
B、27
| ||
C、81
| ||
| D、36 |
