题目内容
已知函数f(x)=xex+x2+ax+b,在点(0,f(0))处的切线方程是x+y-1=0,其中e为自然对数的底数,函数g(x)=lnx-cx+1+c(c>0),对一切x∈(0,+∞),均有g(x)≤1恒成立.
(1)求a,b,c的值;
(2)求证:f(x)+xg(x)>4
-2.
(1)求a,b,c的值;
(2)求证:f(x)+xg(x)>4
| x |
考点:函数恒成立问题,不等式的证明
专题:计算题,证明题,导数的概念及应用,导数的综合应用,不等式的解法及应用
分析:(1)求出f(x)的导数,由切线方程可得,f(0)=1,f′(0)=-1,即可解得a,b;对一切x∈(0,+∞),均有g(x)≤1恒成立,即有lnx-cx+c≤0对x>0恒成立.运用导数求出不等式左边的最大值即可,再由lnx≤x-1,即可得到c;
(2)可运用分析法,结合ex≥x+1,xlnx≥-
,令t=
,即有不等式左边为t4+t2-4t+3-
,运用导数求出最小值,说明它大于0,即可得证.
(2)可运用分析法,结合ex≥x+1,xlnx≥-
| 1 |
| e |
| x |
| 1 |
| e |
解答:
(1)解:函数f(x)=xex+x2+ax+b的导数为
f′(x)=ex+xex+2x+a,
在点(0,f(0))处的切线方程是x+y-1=0,
即有f(0)=1,f′(0)=-1,则b=1,a=-2,
对一切x∈(0,+∞),均有g(x)≤1恒成立,
即有lnx-cx+c≤0对x>0恒成立.
由于(lnx-cx+c)′=
-c(c>0),则lnx-cx+c在x>
递减,在0<x<
递增.
则有ln
-1+c≤0,即为lnc+1≥c,
但lnx+1-x的导数为
-1,在x>1递减,在0<x<1递增,则在x=1处取得极大值,也为最大值,
则lnc+1≤c,故lnc+1=c,解得,c=1,
则有a=-2,b=1,c=1;
(2)证明:要证f(x)+xg(x)>4
-2,
即证xex+x2-2x+1+xlnx-x2+2x-4
+2>0,
即证xex+xlnx-4
+3>0,
由于ex-x-1的导数为ex-1,当x>0递增,x<0递减,则ex≥x+1,
xlnx的导数为lnx+1,当x>
时递增,0<x<
递减,则有x=
处取得极小值也为最小值,且为-
,
则有xex+xlnx-4
+3>x(x+1)-
-4
+3,
令t=
,则上式的右边即为t4+t2-4t+3-
,对它求导,得f(t)=4t3+2t-4,
由于f(0)f(1)<0,则在(0,1)存在一个根t0,易得即为极小值点,也为最小值点,
可得t04+t02-4t0+3-
>0,
则原不等式成立.
f′(x)=ex+xex+2x+a,
在点(0,f(0))处的切线方程是x+y-1=0,
即有f(0)=1,f′(0)=-1,则b=1,a=-2,
对一切x∈(0,+∞),均有g(x)≤1恒成立,
即有lnx-cx+c≤0对x>0恒成立.
由于(lnx-cx+c)′=
| 1 |
| x |
| 1 |
| c |
| 1 |
| c |
则有ln
| 1 |
| c |
但lnx+1-x的导数为
| 1 |
| x |
则lnc+1≤c,故lnc+1=c,解得,c=1,
则有a=-2,b=1,c=1;
(2)证明:要证f(x)+xg(x)>4
| x |
即证xex+x2-2x+1+xlnx-x2+2x-4
| x |
即证xex+xlnx-4
| x |
由于ex-x-1的导数为ex-1,当x>0递增,x<0递减,则ex≥x+1,
xlnx的导数为lnx+1,当x>
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
则有xex+xlnx-4
| x |
| 1 |
| e |
| x |
令t=
| x |
| 1 |
| e |
由于f(0)f(1)<0,则在(0,1)存在一个根t0,易得即为极小值点,也为最小值点,
可得t04+t02-4t0+3-
| 1 |
| e |
则原不等式成立.
点评:本题考查导数的运用:求切线方程和求单调区间、极值和最值,考查不等式的恒成立问题转化为求函数的最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
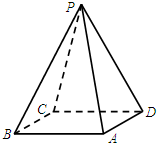 点P为正方形ABCD所在平面外一点,AD=3,PD=2
点P为正方形ABCD所在平面外一点,AD=3,PD=2| 3 |
| A、30° | B、45° |
| C、60° | D、90° |
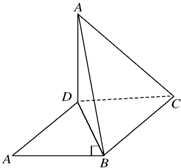 如图,平行四边形ABCD中,AB⊥BD,沿BD将△ABD折起到A′BD,使面A′BD⊥面BCD,连接A′C,则在四面体A′BCD的四个面中,互相垂直的平面有( )
如图,平行四边形ABCD中,AB⊥BD,沿BD将△ABD折起到A′BD,使面A′BD⊥面BCD,连接A′C,则在四面体A′BCD的四个面中,互相垂直的平面有( )