题目内容
斜率为k的直线过点P(0,1),与双曲线3x2-y2=1交于A,B两点.
(1)求实数k的取值范围;
(2)若以AB为直径的圆过坐标原点,求k的值.
(1)求实数k的取值范围;
(2)若以AB为直径的圆过坐标原点,求k的值.
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)由题意,直线的方程为y=kx+1;与3x2-y2=1联立消y得,(3-k2)x2-2kx-2=0;利用二次方程的根与系数的关系求解.
(2)设A(x1,y1),B(x2,y2);由OA⊥OB得x1x2+y1y2=0;从而求解.
(2)设A(x1,y1),B(x2,y2);由OA⊥OB得x1x2+y1y2=0;从而求解.
解答:
解:(1)由题意,直线的方程为y=kx+1;
与3x2-y2=1联立消y得,
(3-k2)x2-2kx-2=0;
则;
;
解得-
<k<-
或-
<k<
或
<k<
;
(2)设A(x1,y1),B(x2,y2);
∵OA⊥OB,
∴x1x2+y1y2=0;
而x1+x2=
,x1x2=
;
故y1y2=1;
故1+
=0,
解得,k=±1.
与3x2-y2=1联立消y得,
(3-k2)x2-2kx-2=0;
则;
|
解得-
| 6 |
| 3 |
| 3 |
| 3 |
| 3 |
| 6 |
(2)设A(x1,y1),B(x2,y2);
∵OA⊥OB,
∴x1x2+y1y2=0;
而x1+x2=
| 2k |
| 3-k2 |
| -2 |
| 3-k2 |
故y1y2=1;
故1+
| -2 |
| 3-k2 |
解得,k=±1.
点评:本题考查了双曲线的性质应用,属于基础题.

练习册系列答案
相关题目
某棱柱如图所示放置,则该棱柱的正视图是( )


A、 |
B、 |
C、 |
D、 |
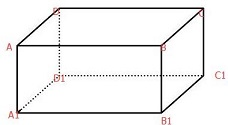 如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=3
如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=3