题目内容
已知函数f（x）=2sin（2x+
）+m，且f（
）=6．
（1）求m的值；
（2）若f（θ）=
，且θ∈（
，
），求sin（4θ+
）的值．
| π |
| 6 |
| π |
| 6 |
（1）求m的值；
（2）若f（θ）=
| 28 |
| 5 |
| π |
| 6 |
| 5π |
| 12 |
| π |
| 3 |
考点：二倍角的正弦
专题：计算题,三角函数的求值
分析：（1）利用函数f（x）=2sin（2x+
）+m，且f（
）=6，即可求出m的值；
（2）求出2sin(2θ+
)=
，再利用同角三角函数的关系，二倍角的正弦公式，即可求sin（4θ+
）的值．
| π |
| 6 |
| π |
| 6 |
（2）求出2sin(2θ+
| π |
| 6 |
| 4 |
| 5 |
| π |
| 3 |
解答：
解：（1）∵f(
)=2sin(
+
)+m=2+m=6，∴m=4．
（2）由f(θ)=
，得2sin(2θ+
)+4=
，即2sin(2θ+
)=
，
∵θ∈(
，
)，∴2θ+
∈(
，π)．
∴cos(2θ+
)=-
=-
，
sin(4θ+
)=2sin(2θ+
)cos(2θ+
)=-
．
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
（2）由f(θ)=
| 28 |
| 5 |
| π |
| 6 |
| 28 |
| 5 |
| π |
| 6 |
| 4 |
| 5 |
∵θ∈(
| π |
| 6 |
| 5π |
| 12 |
| π |
| 6 |
| π |
| 2 |
∴cos(2θ+
| π |
| 6 |
1-sin2(2θ+
|
| 3 |
| 5 |
sin(4θ+
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 24 |
| 25 |
点评：本题考查二倍角的正弦，考查同角三角函数的关系，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
由函数y=ex，y=e及直线x=0所围成的图形的面积为（ ）
| A、1 | ||
B、
| ||
| C、e | ||
| D、2 |
已知集合A={x|1≤2x＜8，x∈N*}，则集合B={x-y|x∈A，y∈A}中元素的个数是（ ）
| A、1 | B、3 | C、5 | D、9 |
设集合A={1，2}，则满足A∪B={1，2，3}的集合B的个数是（ ）
| A、1个 | B、2个 | C、4个 | D、8个 |
以下是定义域为R的四个函数，奇函数的为（ ）
| A、y=x3 | ||
| B、y=2x | ||
| C、y=x2+1 | ||
D、y=
|
函数f（x）=lg（x-1）+
的定义域是（ ）
| 3-x |
| A、（1，3） |
| B、[1，3] |
| C、（1，3] |
| D、[1，3） |
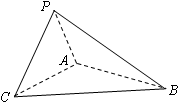如图，平面PAC⊥平面ABC，△PAC是正三角形，∠CAB=90°，AB=2AC．