题目内容
14.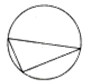 如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)
如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)
分析 根据题意,由题意相邻两块的颜色不同,通过对涂色区域编号,分别选出2种颜色、3种颜色、4种颜色涂色,求出各自的涂色方案种数,即可得到结果.
解答  解:对涂色区域编号,如图:
解:对涂色区域编号,如图:
分别用2色、就是1一色,2、3、4同色,涂色方法为:C52A22=20;
涂3色时,2、3同色,2、4同色,3、4同色,涂色方法是3C53A33=180;
涂4色时涂色方法是A54=120,
所以涂色方案有:20+180+120=320;
故答案为:320.
点评 本题考查排列、组合的实际应用,关键是依据题意,对选用的颜色进行分类讨论.

练习册系列答案
相关题目
5.不等式($\frac{1}{2}$-x)($\frac{1}{3}$-x)>0的解集是( )
| A. | {x|$\frac{1}{3}$<x<$\frac{1}{2}$} | B. | {x|x>$\frac{1}{2}$} | C. | {x|x<$\frac{1}{3}$} | D. | {x|x<$\frac{1}{3}$或x>$\frac{1}{2}$} |
19.下列关于K2的说法正确的是( )
| A. | K2在任何相互独立问题中都可以用来检验有关还是无关 | |
| B. | K2的值越大,两个事件的相关性越大 | |
| C. | K2是用来判断两个分类变量是否有关系的随机变量,只对于两个分类变量适合 | |
| D. | K2的观测值的计算公式为K2=$\frac{n(ad-bc)}{(a+b)(c+d)(a+c)(b+d)}$ |